二階常係數齊次線性微分方程
標準形式
y″+py′+qy=0
特徵方程
r^2+pr+q=0
通解
1.兩個不相等的實根：y=C1e^(r1x)+C2e^(r2x)
2.兩根相等的實根：y=(C1+C2x)e^(r1x)
3.一對共軛復根：r1=α+iβ,r2=α-iβ：y=e^(αx)*(C1cosβx+C2sinβx)
二階常係數非齊次線性微分方程
標準形式
y''+p(x)y'+q(x)y=f(x)
解法
通解=非齊次方程特解+齊次方程通解
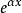二階常係數線性微分方程對二階常係數線性非齊次微分方程形式ay''+by'+cy=p(x)的特解y*具有形式
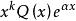二階常係數線性微分方程y*=
其中Q(x)是與p(x)同次的多項式，k按α不是特徵根、是單特徵根或二重特徵根（上文有提），依次取0,1或2.
將y*代入方程，比較方程兩邊x的同次冪的係數（待定係數法），就可確定出Q(x)的係數而得特解y*。
多項式法：
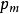二階常係數線性微分方程設常係數線性微分方程y''+py'+qy =pm(x)e^(λx)，其中p，q，λ是常數，pm(x)是x的m次多項式，令y=ze^(λz) ，則方程可化為：
F″(λ)/2!z″+F′(λ)/1!z′+F(λ)z=pm(x) ，這裡F(λ)=λ^2+pλ+q為方程對應齊次方程的特徵多項式。
升階法：
設y''+p(x)y'+q(x)y=f(x)，當f(x)為多項式時，設f(x)=a0x^n+a1x^(n-1)+…+a(n-1)x+an，此時，方程兩邊同時對x求導n次，得
y'''+p(x)y''+q(x)y'=a0x^n+a1x^(n-1)+…+a(n-1)x+an……
y^(n+1)+py^(n)+qy^(n-1)=a0n!x+a1(n-1)!
y^(n+2)+py^(n+1)+qy^(n)=a0n!
令y^n=a0n!/q(q≠0),此時，y^(n+2)=y^(n+1)=0。由y^(n+1)與y^n通過倒數第二個方程可得y^(n-1)，依次升階，一直推到方程y''+p(x)y'+q(x)y=f(x)，可得到方程的一個特解y(x)。
微分運算元法：
微分運算元法是求解不同類型常係數非齊次線性微分方程特解的有效方法，使用微分運算元法求解二階常係數非齊次線性微分方程的特解記憶較為方便，計算難度也可降低。引入微分運算元d/dx=D，d^2/dx^2=D^2，則有 y'=dy/dx=Dy，y''=d^2y/dx^2=D^2y
於是y''+p(x)y'+q(x)y=f(x)可化為(D^2+pD+q)y=f(x)，令F(D)=D^2+pD+q，稱為運算元多項式，F(D)=D^2+pD+q即為F(D)y=f(x)，其特解為y=f(x)/F(D) 。
降解法：
如果已知線性微分方程對應齊次方程的一個特解，就可以用降解法求出其解，線性齊次微分方程的特解也可以用降階法求出 。
