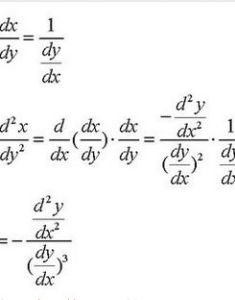代數記法
二階導數記作y‘’=d^2y/dx^2即y‘’=(y‘)’。例如:y=x^2的導數為y=2x,二階導數即y=2x的導數為y=2。
幾何意義
(1)切線斜率變化的速度(2)函式的凹凸性(例如加速度的方向總是指向軌跡曲線凹的一側)
這裡以物理學中的瞬時加速度為例:
根據定義有a=(v'-v)/Δt=Δv/Δt
可如果加速度並不是恆定的某點的加速度表達式就為:
a=limΔt→0Δv/Δt=dv/dt(即速度對時間的一階導數)
又因為v=dx/dt所以就有
a=dv/dt=d^2x/dt^2即元位移對時間的二階導數
將這種思想套用到函式中即是數學所謂的二階導數
f'(x)=dy/dx(f(x)的一階導數)
f''(x)=d^2y/dx^2=d(dy/dx)/dx(f(x)的二階導數)
相關補充
二階導數是比較理論的、比較抽象的一個量,它不像一階導數那樣有明顯的幾何意義,因為它表示的是一階導數的變化率。在圖形上,它主要表現函式的凹凸性,直觀的說,函式是向上突起的,還是向下突起的。套用
 二階導數
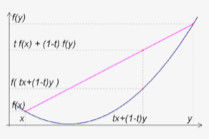
二階導數如果一個函式f(x)在某個區間I上有f''(x)(即二階導數)>0恆成立,那么對於區間I上的任意x,y,總有:
f(x)+f(y)≥2f[(x+y)/2],如果總有f''(x)<0成立,那么上式的不等號反向。
幾何的直觀解釋:如果一個函式f(x)在某個區間I上有f''(x)(即二階導數)>0恆成立,那么在區間I上f(x)的圖象上的任意兩點連出的一條線段,這兩點之間的函式圖象都在該線段的下方,反之在該線段的上方。