多項式
在數學中,由若干個單項式相加組成的代數式叫做多項式(若有減法:減一個數等於加上它的相反數)。多項式中的每個單項式叫做多項式的項,這些單項式中的最高項次數,就是這個多項式的次數。
對於比較廣義的定義,1個或0個單項式的和也算多項式。按這個定義,多項式就是整式。實際上,還沒有一個只對狹義多項式起作用,對單項式不起作用的定理。0作為多項式時,次數定義為負無窮大(或0)。單項式和多項式統稱為整式。
多項式中不含字母的項叫做常數項。如:5X+6中的6就是常數項。
定義
二次多項式是指這個多項式的項數超過1,且最高次方數為2的多項式。
一元二次多項式
簡介
一元二次多項式(quadratic polynomial withone variable)最常見的一種多項式.只含一個變數字母且各項最高次數為2的多項式稱為一元二次多項式,它的標準形式為ax^2+bx+c(a≠0),式中a ,b,c為常數。
因式分解
對於二次多項式 aX +bX+c(a≠0)
當△=b -4ac≥0時,設aX +bX+c=0的解為X,X
則原式可化為a(X -(X+X)X+XX)=a(X-X)(X-X)。
例題
求一個二次多項式f(x),使得f(1)=0,f(2)=3,f(-3)=28。
因為f(x)是一個二次多項式,所以可設:f(x)=ax^2 + bx + c
當x=1時,f(1)=0;
x=2時,f(2)=3;
x=-3時,f(-3)=28
代入得三元一次方程組:
a + b + c = 0
4a + 2b + c = 3
9a - 3b + c = 28
解得:a = 2,b = -3,c = 1所以,f(x) =2x^2 -3x +1。
二次多項式擬合法的套用
GNSS測量得到測量點的3維坐標,受技術條件的限制,從20世紀80年代末GPS技術引進後,只是使用了GPS測量的平面2維成果,高程測量成果一直沒有大量使用。隨著全球高精度重力場模型的確定及基礎理論上的突破,經過大量的實驗,GNSS測量求取正常高成為現實。其原理是利用GPS測量得到的大地高結合高程異常改正模型,計算待定點的高程異常,從而確定地麵點的正常高。因此,高程異常模型的正確建立是進行GNSS高程測量的先決條件。
曲面擬合法是GNSS高程測量中建立高程異常模型最常用的幾何方法之一,其思想是認為高程異常在一定範圍內變化平緩的前提下,將高程異常近似看作是一定範圍內各點坐標的曲面函式,用這一擬合函式來計算其他GPS點的高程異常和正常高。GNSS高程異常曲面擬合方法可分平面擬合法、多項式曲面擬合法、多面函式擬合法等。
在測區面積較大,地勢變化較為平緩的測區,採用二次多項式擬合法、多面函式擬合法兩種方法確定的區域高程異常模型能較好地擬合出測區起伏變化的似大地水準面,且精度相當。
二次多項式擬合法的數學模型為:
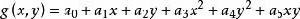 二次多項式
二次多項式