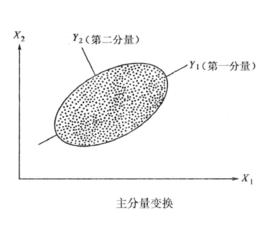
簡介
主分量變換也稱K-L變換,是一種線性變換,是就均方誤差最小來說的最佳正交變換;是在統計特徵基礎上的線性變換。對於遙感多光譜圖像來說,波段之間往往存在很大的相關性,從直觀上看,不同波段圖像之間很相似。從信息提取角度看,有相當大的數據量是多餘的,重複的。
主分量變換目的
進行主分量變換等特徵變換的目的是將原始圖像通過一定的數字變換生成一組新的特徵圖像,這一組新圖像信息集中在少數幾個特徵圖像上,這樣,數據量有所減少,達到消除相關係數,進行有效的特徵選擇和減少波段特徵空間維數,達到數據壓縮的目的。
主分量變換原理
主分量變換也叫主成份分析或者主分量分析。是在統計特徵基礎上的一種多維(如多波段)正交線性變換。變換依據的準則是最小均方誤差(K-L準則),即使經過反變換而恢復的影像X與原影像之間的均方差最小。K-L 變換能夠把原來多個波段中的有用信息儘量集中到數目儘可能少的特徵圖像組中去,達到數據壓縮的目的;同時,K-L 變換還能夠使新的特徵圖像之間互不相關,也就是使新的特徵圖像包含的信息內容不重疊,增加類別的可分性。
主分量變換計算步驟
1、 計算多光譜圖像的均值向量M和協方差矩陣∑。
2、計算矩陣∑的特徵值λ和特徵向量φ(r=1,2,…,m),m為多光譜圖像的波段數。
3、將特徵值λ,按由大到小的次序排列,即λ>λ>...>λ。
4、選擇前n個特徵值對應的n個特徵向量構造變換矩陣Φ。
5、根據Y=ΦX進行變換,得到的新特徵影像就是變換的結果,X為多光譜圖像的一個光譜特徵矢量。
主分量變換作用
進行主分量變換計算後,新的特徵圖像組Y就是一個特徵維數得到壓縮的n維特徵矢量(n<m)。原始數據經過主分量變換後,其方差分布主要集中在前面幾個特徵,方差的大小反映了模式的散布情況。由於特徵向量的方向指向特徵空間中集群分布的結構軸方向,所以該變換的幾何意義是把原始特徵空間的特徵軸旋轉到平行於混合集群結構軸的方向上去。使得第一主分量方差分布最廣,集中最多信息,第二分量次之。
主分量變換優點
1、變換後的矢量Y的協方差矩陣是對角陣,對角矩陣表明新特徵矢量之間彼此不相關。
2、經過主分量變換後得到幾個變數,可以證明此時具有的均方誤差在所有正交變換中是最小的。由於n<m,這樣就用比較少的變數代替了原來的幾個變數,實現了數據壓縮。主分量變換後,有的特徵影像反差拉大,信息集中,整個影像上離散度變大;而另一些特徵影像上離散度變小,出現更多的噪聲。