圖像信號的二維小波變換
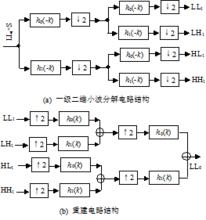
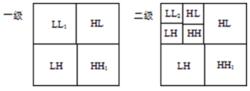
對於二維圖像信號，可以用分別在水平和垂直方向進行濾波的方法實現二維小波多解析度分解，如圖41.53所示為二維圖像的(一級)分解和重建電路結構圖。圖41.54所示為相應的二維頻域劃分示意圖。每經過一級分解，當前頻帶LL 被分為4個子帶LL 、LH 、HL 和HH 。其中低頻帶LL 對應於圖像在下一尺度的概貌，其餘3個子帶分別反映圖像在水平、垂直和對角線方向的高頻細節信息。圖41.55為“女郎”像經過二級分解的結果。
圖像的小波變換編碼圖41.53 二維圖像的(一級)分解和重建電路結構
圖像的小波變換編碼圖41.54 一級、二級二維分解的頻帶劃分示意圖
圖像的小波變換壓縮編碼
圖像信號經過小波多解析度分解之後成為若干不同頻帶的信號，這些頻帶信號具有不同的特點，因此為壓縮編碼提供了很好的依據。
（1）DCT+矢量量化的壓縮
經過小波多解析度分解之後，所得到的低頻部分仍然保持原圖像的概貌，因此可以使用JPEG的ADCT編碼對它進行壓縮。對於高頻部分，可以發現三個方向的子帶各自包含了原圖像中在水平、垂直和對角線方向的高頻分量，因而其中的大部分區域變化幅度較低。且能量較低，而能量高，變化大的區域集中在圖像內物體的邊緣部分，它保持著物體的結構特徵，參見圖41.55。因此可以根據高頻帶內的這些分布特點採用高效的矢量量化方法進行壓縮。
圖像的小波變換編碼圖41.55 二級分解例子
（2）嵌入式零樹編碼EZW
EZW算法是由J.M.Shapiro提出的小波變換圖像壓縮編碼方法。它主要包括4個步驟：
① 小波多解析度分解
利用小波多解析度分解，將原圖像變換為一個低頻帶LL 和3 n個高頻帶部分LH 、HL 和HH ， j=n，…，2，1。 n為分解的級數。
② 零樹編碼
根據圖像分解後係數在不同尺度之間的自相似性預測無效係數出現的位置。
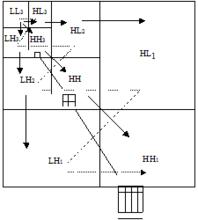
首先用四杈樹建立在不同解析度下子帶係數的父子關係，如圖41.56所示。如果從某個係數起，它的後代全為零，並且該係數的父節點非零，則該係數稱為一個零樹根，它和它的所有後代節點構成一個零樹。
由於高頻部分對應於圖像中邊緣部分，因此在不同尺度下係數的分布在空間上存在對應關係，即自相似性。根據這一性質，對變換係數量化後，出現零樹的可能性很大，當按照圖41.56虛線的掃描次序對所有子帶進行掃描時，可以分辨4類不同的係數：零樹根、正值、負值和孤立零值。於是可以有效地記錄所有非零係數的位置，即所謂有效圖，這就是所謂的零樹編碼得以壓縮的主要原因。
③ 比特面逐步近似量化
為了得到嵌入式碼流，使用類似於比特面的編碼傳輸，按2的冪次遞減的次序對各子帶的變換係數進行掃描量化。根據作用的不同，將掃描分為主掃描和從掃描，其中主掃描用以搜尋量化步長改變後出現的新的零樹根，副掃描則用於對已經找到的非零係數(有效係數)進行細一層量化修正。當從掃描完成後將量化步長進行降冪再進行下一輪主掃描，依次反覆進行，最後達到所希望的量化水平。
圖像的小波變換編碼圖41.56 子帶間父子關係以及子帶掃描順序(虛線)
④ 自適應算術編碼
為了提高壓縮效率，採用自適應算術編碼對掃描輸出符號進行編碼。
由於EZW算法具有良好的編碼性能，因而受到人們廣泛的關注，先後出現了許多改進的算法，例如SPIHT算法改進了逐漸傳輸方案，使得即使不採用算術編碼也能達到與EZW相當的壓縮效果；此外還有一些利用彩色分量的相關性進行EZW壓縮以及對任意形狀的對象進行EZW壓縮的算法。EZW算法的主要思想已經被MPEG-4的靜止圖像編碼部分以及JPEG2000等國際標準採用。由此可見其重要地位。
