不適定問題數值解法

反問題,不適定性及其與第一類運算元方程的聯繫，基於運算元廣義逆理論的各種推廣，幾種提高正則解精度和計算效率的疊代正則化方法、離散正則化方法，各種正則化算法的數值實現，帶有工程、物理與經濟套用背景有啟發性的實例，在附錄中給出了最近的國內外研究成果和示範性MALAB語言源程式。雙曲方程不適定問題的數值求解方法，討論了這類基本問題的不適定性，提出了數值求解方面的逼近問題，給出了討論問題的基本空間，論證了基本空間為Ｈｉｂｅｒｔ空間及基本空間上關於連續映射與收斂性方面的若干結果，從而為討論逼近問題的適定性與收斂性奠定了基礎．

不適定問題數值解法

正文

如果某個數學問題的解對定解數據的擾動極敏感，即不是連續地依賴於定解數據，則稱該問題是不適定的。
在較長一段時間內，不適定問題被認為沒有物理背景，因而沒有引起足夠的重視。最近幾十年來，提出了不少具有實際意義的不適定問題，其數學理論和近似數值解法的研究也得到蓬勃的發展。
典型的不適定問題有：第一類運算元(積分)方程、拉普拉斯方程的初值問題、熱傳導方程逆時向的初值問題、波動方程的狄利克雷問題、求解微分方程係數的反問題等等。
不適定問題可以看為極度病態的問題。在n 維歐氏空間中考察線性方程Au=ƒ,其中A是線性運算元。設AA的特徵值為1=λ1≥λ2≥…≥λn≥0。若A非奇異,則λn>0,方程有惟一解。但若λn很小,則此方程的條件數(1/λn)1/2很大,方程是病態的。現在在可分的希氏空間H中討論這個方程。若λn>0，且當n→ 時，λn→0，則上述方程就是第一類運算元方程。
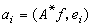設{ei}為AA的特徵元素組成的完備基,則成立展開式,其中。此時方程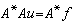的形式解為：
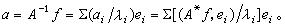設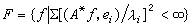,可知A-1僅定義在F上,亦即僅當ƒ∈F時，方程才存在解u=A-1ƒ。
如果已知定解數據ƒ的近似值為ƒδ,則可能，此時A-1ƒδ無意義,即方程無解。即使ƒδ∈F,此時雖存在,但由於A-1無界，也不能通過δ=‖ƒ-ƒδ‖加以估計。所以，直接求解 Auδ=ƒδ不能得到有任何確保精度的近似解。這就是求解不適定問題的困難所在。
為了求得具有一定精度的近似解，已經提出了許多有效的解法。20世紀60年代，蘇聯數學家A.H.吉洪諾夫提出的正則法是較為重要的一種。設R是D(R)→H的對稱運算元，D(R)在H中處處稠密，且存在常數c>0，對任意的v∈D(R)，成立(Rv,v)≥с(v,v)>0（在一般情況下，要求R 非負，且除了H 的一個有限維子空間外上式成立即可）。將滿足

的極值點uδ作為對應於近似數據ƒδ的近似解。上述條件極值點uδ也是下列無約束極值問題

的解，其中α(δ)是拉格朗日乘子。由變分原理即得

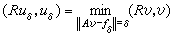
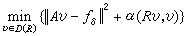
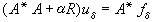
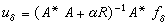由於AA+αR是對稱正定算子,((AA+αR)v,v)≥αс(v,v)，所以其逆存在，。可以證明,當δ→0時，‖u-uδ‖→0。
正則法的實質在於，對原不適定問題中的運算元附加一個適當的小擾動項αR，使之正則化（穩定化），即帶有擾動項的問題是適定的。在不適定問題的許多有效解法中，都以某種方式體現了這種正則化思想。

配圖

相關連線