簡介
20 世紀50 年代,前蘇聯數學家吉洪諾夫(A.H.Tychonoff) 提出的正則化方法是較為重要的一種。
例舉
不適定問題的最典型的例子是拉普拉斯方程的柯西問題。其他的一些不適定問題有:第一種弗雷德霍姆積分方程、反向熱導方程的邊值問題、波動方程的狄利克雷問題和不少微分方程的反問題,等等。
第一類弗雷德霍姆積分方程
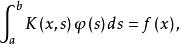 不適定問題
不適定問題其中,a,b 是常數,K(x,s)、f(x) 都是已知函式,φ(s) 是未知的。一般說來該方程是無解的;即使有解,解也不一定唯一;而且即使存在唯一解,解也是不穩定的。對於一個給定的定解問題,如果條件 ③不滿足,那么就稱為阿達馬(J.Hadamard)意義下的不適定問題,如阿達馬例。其他一些不適定問題有逆向熱傳導問題以及其他反問題等。
套用
套用當初
在一段時間裡,人們認為不適定問題不反映任何物理現象,而無研究價值。
套用領域
隨著生產和科學技術的發展、套用的迫切需要,各種各樣的不適定問題出現在許多領域中,如地球物理、連續介質力學、自動控制、大氣物理、全息照相、天體力學、熱力學、 電磁學、 熱擴散理論、電子聚焦問題等,這些問題一般沒有精確解,為了求得具有一定精度的穩定近似解,已經提出許多有效的解法。
拉普拉斯方程的柯西問題、波動方程對非空向 (nonspace-like)初始流形的初值問題,在地球物理勘探的資料解釋和數據處理中,皆具有重要的套用。
發展
求解條件
由於這些問題的數據常常是通過測量給出的近似值,問題通常沒有精確解。因此,人們就去尋找滿足方程但只是近似地適合定解條件的所謂近似解,或近似地滿足方程的近似解。當然,這些近似解一般是沒有惟一性的,但是若對近似解所在的函式類加以適當的限制,例如緊性的限制,便可以保證近似解對數據的連續依賴性。
求解備註
在求問題數值解時,須明確在什麼度量下對近似解加以緊性限制,使問題變為適定,且切合實際的需要。

