 三弦定理
三弦定理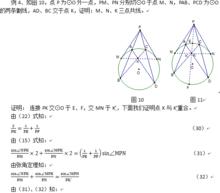 三弦定理
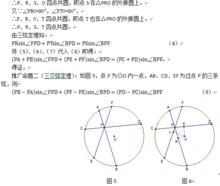
三弦定理用圖表述;圓上一點A,引出三條弦AB(左)、AC(右)、及中間弦AD,BC與AD交於P,根據《三弦定理》,有以下關係,
ABsin∠CAD +ACsin∠BAD= ADsin∠BAC。
證明如下;連BD、CD, 由圓的相交弦定理→△ABP∽△CDP→AB/CD=AP/CP→AB·CP=CD·AP→
AB·CP-CD·AP=0→同理→AC·BP-BD·AP=0, 所以有AB(AB·CP-CD·AP)=0, AC(AC·BP-BD·AP)=0,兩式相加→AB·AB·CP + AC·AC·BP=AB·CD·AP +AC·BD·AP=AP(AB·CD+AC·BD)=AP·BC·AD⑴(托氏定理)。
由AC外分∠BAP, 由《分角定理》→(sin∠CAP/ sin∠BAC)=(CP/BC) ·(AB/AP), →
(ABsin∠CAP/ sin∠BAC)=(CP/BC) ·(AB·AB/AP)⑵, 同理有, 由AB外分∠CAP, 由《分角定理》→
(ACsin∠BAP/ sin∠BAC)=(BP/BC) ·(AC·AC/AP)⑶, 由⑵+⑶→
(ABsin∠CAP+ ACsin∠BAP) / sin∠BAC=( AB·AB·CP+ AC·AC·BP)/BC·AP,由⑴→
( AB·AB·CP+ AC·AC·BP)/BC·AP=AD, 所以(ABsin∠CAP+ ACsin∠BAP) / sin∠BAC=AD, 所以,
ABsin∠CAP+ ACsin∠BAP= ADsin∠BAC。證畢。
《三弦定理》是托勒密定理的一種特殊形式,但他的逆定理證明遠比托勒密逆定理簡單,因此廣為流傳。
