基本介紹
薩蒙(Salmon, 1819-1904年)是英國數學家。初期從事綜合幾何研究,後研究代數形式的不變數與共變數理論在曲線、曲面幾何中的套用。先後寫出幾十篇論文和四本重要的教科書《圓錐曲線》、《高階平面曲線》、《三維解析幾何》等,在西歐各國出版,廣泛流傳,影響較大。薩蒙在數學上的其它貢獻還有:三次曲面上的27條直線的發現;限定條件下的曲面性質;代數方程重根的條件等。
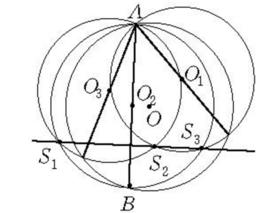
薩蒙定理是關於點共線和距離成比例的兩個定理:
1.自圓上一點引三弦,並以它們各為直徑畫圓,則所畫三圓的兩兩相交的三個與A不同的交點共線(如圖)。
2.圓心O至A,B兩點的距離與A至B的極線b的距離及B至A的極線a的距離成比例。
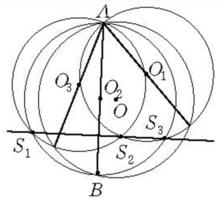 圖1
圖1點共線及其證明
從圓上任意一點引三條弦,並分別以這三條弦為直徑作圓,則所作三圓的其它三個交點共線。
證明 設P為圓O上任一點,PA、PB、PC是任意作的弦,分別以PA、PB、PC為直徑作圓O、O、O,其中⊙O與⊙O、⊙O與⊙O、⊙O與⊙O的另一交點分別為D、E、F。
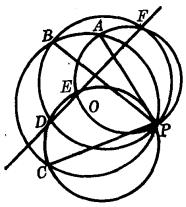 圖2
圖2首先連線DB、DC,在⊙O與⊙O中,
∵ PB、 PC為直徑,
∴∠PDB=∠PDC= 90°,
證得B、D、C三點共線,也即PD⊥BC於D。
同法可證PE⊥CA於E,PF⊥AB於F。
又P、A、B、C四點本來共圓,因此問題成為自△ABC外接圓上任-一點P作PD⊥BC、PE⊥CA、PF⊥AB垂足分別為D、E、F,要證D、B、F三點共線。而這就是西摩松線,所以本命題成立 。
距離成比例及其證明
圓心O到A、B兩點的距離與A到B的極線b及B到A的極線a的距離成比例。
該定理為英國數學家G.Salmon所發現,它是極和極線理論中的一個基本定理。
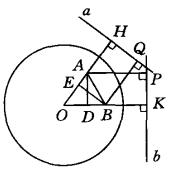 圖3
圖3如圖3,直線a、b分別是點A、B的極線,OA⊥a於H,OB⊥b於K,AP是A到極線b的距離,BQ是B到極線a的距離。作AD⊥OB於D,BE⊥OA於E,則A、E、D、B四點共圓,於是有
OD·OB=OE·OA, ①
又 OB·OK=R²=OA·OH,②
②一①得 OB(OK-OD)=OA(OH-OE),
即 OB·AP=OA·BQ,
OA∶OB=AP∶BQ 。