簡介
概念定義
用符號“=”連線的式子叫做等式。
用符號“<”（或“≤”），“>”（或“≥”）,“≠”連線的式子叫做不等式。(不等式中可以含有未知數，也可以不含。)
用不等號連線的，含有一個未知數，並且未知數的次數都是1，係數不為0，左右兩邊為整式的式子叫做一元一次不等式（linear ineqality with one unknown）。
不等式性質
（1）不等式的兩邊都加上（或減去）同一個數(或式子)，不等號的方向不變。
（2）不等式的兩邊都乘以（或除以）同一個正數，不等號的方向不變。
（3）不等式的兩邊都乘以（或除以）同一個負數，不等號的方向改變。
數字語言簡潔表達不等式的性質——
【1.性質1：如果a>b,那么a±c>b±c)】
【2.性質2：如果a>b，c>0，那么ac>bc(或a/c>b/c)】
【3.性質3：如果a>b，c<0，那么ac
一般步驟
（1）去分母 （運用不等式性質2、3）
（2）去括弧
（3）移項 （運用不等式性質1）
（4）合併同類項。
（5）將未知數的係數化為1 （運用不等式性質2、3）
（6）有些時候需要在數軸上表示不等式的解集
不等式解集
一個有未知數的不等式的所有解，組成這個不等式的解集。例如﹕不等式x-5≤-1的解集為x≤4；不等式x﹥0的解集是所有正實數。求不等式解集的過程叫做不等式。
將一元一次不等式化為ax>b的形式
(1)若a>0，則解集為x>b/a。
(2)若a<0，則解集為x
表示
（1） 用不等式表示：一般地，一個含未知數的不等式有無數個解，其解集是一個範圍，這個範圍可用最簡單的不等式表達出來，例如：x-1≤2的解集是x≤3。
（2） 用數軸表示：不等式的解集可以在數軸上直觀地表示出來，形象地說明不等式有無限多個解，用數軸表示不等式的解集要注意兩點：一是定邊界線；二是定方向。
（3）能使不等式成立的未知數的值，叫做不等式的解。
不等式組
（1） 一般地，關於同一個未知數的幾個一元一次不等式合在一起，就組成一個一元一次不等式組。
（2）一元一次不等式組中各個不等式的解集的公共部分，叫做這個一元一次不等式組的解集。求不等式組解集的過程，叫做解不等式組。
1. 代數式大小的比較:
（1） 利用數軸法;
（2） 直接比較法;
（3） 差值比較法;
（4） 商值比較法；
（5） 利用特殊比較法。（在涉及代數式的比較時，還要適當的使用分類討論法）
綜合運用
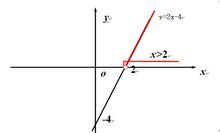
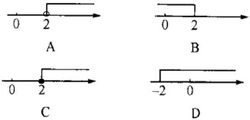用數軸法解一元一次不等式一般先求出函式表達式，再化簡不等式求解。
解題步驟
一元一次不等式（1） 求出每個不等式的解集；
（2） 求出每個不等式的解集的公共部分；（一般利用數軸）
（3） 用代數符號語言來表示公共部分。（也可以說成是聲明結論）
常見解法
等式一元一次不等式如果
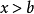一元一次不等式（1） 關於x不等式組{x>a} {x>b}的解集是：
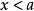一元一次不等式（2） 關於x不等式組{x
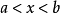一元一次不等式（3） 關於x不等式組{x>a} {x
（4） 關於x不等式組{xb}的解集是空集。
以上取解集的方法可歸納為：兩大取大，兩小取小，大小小大取中間，大大小小無解
特殊不等式組解
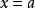一元一次不等式（1） 關於x不等式（組）：{x≥a} { x≤a}的解集為：
（2） 關於x不等式（組）：{xa} 的解集是空集。
一元一次不等式不同點：一元一次不等式表示不等關係，一元一次方程表示相等關係；一個是運用等式的基本性質，另一個則是不等式的基本性質。
相同點：二者都是只含有一個未知數，未知數的次數都是1，左右兩邊都是整式。一般步驟都是：去分母；去括弧；移項；合併同類項；將未知數的係數化為1
例題解析
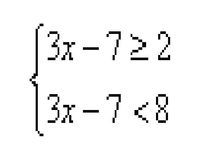一元一次不等式(1) 2x－1<4x+13；
(2)（5x+3）≤x－3（1－2x）.
解 （1）2x－1<4x+13，
2x－4x<13+1，
－2x<14，
x>－7.
（2）2（5x+3）≤x－3（1－2x），
10x+6≤x－3+6x，
3x≤－9，
x≤－3.
練習
1．下列不等式中，是一元一次不等式的有[ ]
A．3x(x+5)>3x2+7；
B．x2≥0；
C．xy-2<3；
D．x+y>5．
2．不等式6x+8>3x+8的解是[ ]
3．3x-7≥4x-4的解是[ ]
A．x≥3；
B．x≤3；
C．x≥-3；
D．x≤-3．
4．若|m-5|=5-m，則m的取值範圍是[ ]
A．m>5；
B．m≥5；
C．m<5；
D．m≤5．
[ ]
A．x>15；
B．x≥15；
C．x<15；
D．x≤15．
6．若關於x的方程3x+3k=2的解是正數，則k的值為[ ]
C．k為任何實數；
D．以上答案都不對．
7．下列說法正確的是[ ]
A．x=2是不等式3x>5的一個解；
B．x=2是不等式3x>5的解；
C．x=2是不等式3x>5的唯一解；
D．x=2不是不等式3x>5的解．
[ ]
A．y>0；
B．y<0；
C．y=0；
D．以上都不對．
9．下列說法錯誤的是[ ]
D．x<3的正數解有有限個．
[ ]
A．x≤4；
B．x≥4；
[ ]
A．x<-2；
B．x>-2；
D．x<2；
D．x>2，
[ ]
A．大於2的整數；
B．不小於2的整數；
D．2；
D．x≥3．
[ ]
A．無數個；
B．0和1；
C．1；
D．以上都不對．
[ ]
A．x>1；
B．x≤1；
C．x≥1；
D．x.>1．
[ ]
A．2x-3x-3<6，-x<9，x>-9；
B．2x-3x+3<6，-x<3，x>-3；
C．2x-3x+1<6，-x<5，x<-5；
D．2x-3x+3<1，-x<-2，x<2．
(二)解一元一次不等式
一元一次不等式26．3x-2(9-x)>3(7+2x)6x)．
27．2(3x-3(4x+5)≤x-4(x-7)
28．2(x-1)>3(x-1)-x-5．
29．3[-2(y-7)]≤4y．
31．15-(7+5x)≤+(5-3x)．
對於任意兩個實數a,b,關係式是a>b,a=b,a
並且規定:
當a-b>0時,有a>b,
當a-b=0時,有a=b:
當a-b<0時,有a
試題列舉
1、一本英語書98頁,孟濤讀了7天(一周)還沒讀完,而張浩不到一周就讀完了，張浩平均每天比孟濤多讀3頁，問孟濤每天讀多少頁?
解：設孟濤每天讀x頁，則張浩讀(x+3)頁，由題意，得：
{98/x>7
{98/(x+3)<7
解得：11<14
∴孟濤每天讀12或13頁
∴x+3=15或16頁
∴張浩每天讀15或16頁
2、把一些書分給幾個學生，如果每人分3本，那么餘8本；如果前面的每個學生分5本，那么最後一人就分不到3本。問這些書有多少本？學生有多少人？
解：設學生有x人 ，由題意，得：
{3x+8-5(x-1)≥0
{3x+8-5(x-1)<3
解得：5
∵由於學生的數量x只能取整數，不為小數。
∴x=6
∴書本有：3×6+8=26（本）
3、用每分鐘抽1.1噸水的A型抽水機來抽池水，半小時可以抽完；如果改用B型抽水機，估計20分鐘到22分可以抽完。B型抽水機比A型抽水機每分鐘約多抽多少噸水？
解：設B型每分鐘抽x噸，由題意，得：
{20x≤1.1*30
{22x≥1.1*30
解得：1.5≤x≤1.65
∴1.5-1.1≤x-1.1≤1.65-1.1
4、一個長方形足球場的長為X米，寬為70米，如果它的周長大於350米，面積小於7650平方米，求X的取值範圍，並判斷這個球場是否可以作為國際足球比賽（註：用於國際比賽的足球場的長在100至110米之間，寬在64至75米之間。
解：設長為x米。
{2x+70*2>350
{x*70<7650
解得：55<109.3
所以，可以
5、有紅、白顏色的球若干個，已知白球的個數比紅球少，但白球的兩倍比紅球多，若把每一個白球都記作數2，每一個紅球都記作數3，則總數為60，求白球和紅球各幾個？
解：設白球數量為X個，則紅球數量為（60-2x）/3個。
{x<(60-2x)/3①
{2x>(60-2x)/3②
解得：①：x<12
②：x>15
so：12<15
10<紅球><16
又因為都為整數所以：
白球：13或14 紅球：
6、一次考試共有25道選擇題，做對一題得4分，做錯一題減2分，不做得0分，若小明想確保考試成績在60分以上，那么，他至少做對X題，應滿足的不等式是什麼？
7、某公司需刻錄一批光碟（總數不超過100張），若請專業公司刻錄，每張需10元（包括空白光碟費）；若公司自刻，除設備租用費200元以外，每張還需成本5元（空白光碟費）。問刻錄這批光碟，是請專家公司刻錄費用省，還是自刻費用省？
8、某校辦廠生產了一批新產品，現有兩種銷售方案，方案一：在這學期開學時售出該批產品，可獲利30000元，然後將該批產品的投入資金和已獲利30000元進行再投資，到這學期結束時再投資又可獲利4.8%;方案二:在這學期結結束時售出該批產品,可獲利35940元,但要付投入資金的0.2%作保管費，問：
（1）當該批產品投入資金是多少元時，方案一和方案二的獲利是一樣的？
（2）按所需投入資金的多少討論方案一和方案二哪個獲利多。 9、某校校長暑假帶領學生去參加科技夏令營。甲旅行社說：“如果校長買全票一張，則其餘學生可享受半折優惠”。乙旅行社說：“ 包括校長在內，全部按全票價六折優惠”已知全票價為240元，請你就學生人數說明哪家旅行社更優惠？（方案問題）
