概念
一般地,關於兩個未知數的幾個二元一次不等式合在一起,就組成一個二元一次不等式組。
解法
二元一次不等式(組)的解集
滿足二元一次不等式(組)的x和y的取值構成有序實數對(x,y),所有這樣的有序實數對(x,y)構成的集合稱為二元一次不等式(組)的解集。二元一次不等式(組)的解集是有序實數對,而點的坐標也是有序實數對,因此,有序實數對就可以看成是平面內點的坐標,進而,二元一次不等式(組)的解集就可以看成是直角坐標系內的點構成的集合。
二元一次不等式的解法同樣有代入法和加減法。
不等號方向相同時,兩式子才能相加,即想辦法把兩式子化成不等號方向相等就行了,
如2x+y>10……(1)
x+y<5…………(2)
把(2)式化成
-x-y+5>0……(3)
這時候(1)和(3)不等號方向相同,式子兩邊可以相加
(2x+y)+(-x-y+5)>10+0
解得x>5
(3)兩邊×2,得-2x-2y+10>0……(4)
(1)和(4)式子兩邊相加
(2x+y)+(-2x-2y+10)>10+0
解得y<0
或,把(2)式化成
x<5-y……(3)
解設x=5-y
把x=5-y代入(1)
2×(5-y)+y>10
解得y<0
解設y=0
把y=0代入(3)
x<5-0
x<5
因為在(3)中y前是負號
所以x>5
(此方法較為複雜,所以還是請用加減法)
用加減法解不等式的時候,不用去記住很多代入法要注意的小技巧,特別是考試時比較緊張,如果要記住太多很容易出錯的。這種相加法,用熟之後過程可以不用這么繁複,可以少寫一兩步。
特別注意,根據不等式性質,不等號方向相同的兩式子,只能相加,不能相減。
不等號方向相反時,兩邊才能相減,相減後的不等號方向與被減式相同。實際這跟兩式相加一樣的,只要把式子兩邊交換,">號"會變"<"號。不過這方法不嚴謹,只能用於選擇填空,用於做大題會被判錯的。而且比兩式相加容易出錯,所以一開始就乖乖做兩式相加好了,等熟練了以後,做選擇填空才用兩式相減。
舉例,2x+y>10……①
x+y<5…………②
①-②,不等號取> 可理解為:①+(-②)
(2x+y)-(x+y)>10-5
得x>5
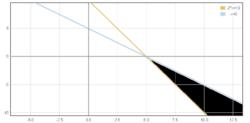 函式圖像
函式圖像解的結果並不能用x>5,y<0表示,以上解法並不準切,畫出圖形可以知道,在x>5,y<0的區域內並不都是不等式組的解。如下圖黑色部分才是不等式組的解集。
套用題
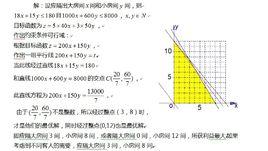
三門縣為促進青蟹養殖業的發展,決定對青蟹養殖戶提供政府補貼。設青蟹的市場價格為X元/千克,政府補貼為Y元/千克,根據市場調查,現在每日市場的青蟹供應量與日需求量正好相等,應滿足等式8(X+Y)=582-3X。為使市場價格不高於50元/千克,那么每千克青蟹政府至少要補貼給養殖戶多少元?
8(x+y)=582-3x
11x+8y=582
又因為x不大於50
x≤50
y≥4
所以至少4元/Kg
政府至少要補貼給養殖戶4元/千克