一位全加器

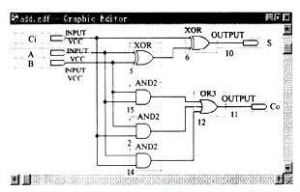
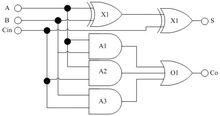
全加器是能夠計算低位進位的二進制加法電路。與半加器相比,全加器不只考慮本位計算結果是否有進位,也考慮上一位對本位的進位,可以把多個一位全加器級聯後做成多位全加器.

一位全加器

一位全加器(FA)的邏輯表達式為：

Ai	Bi	Ci-1	Si	Ci
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

S=A⊕B⊕Cin

Co=ACin+BCin+AB

其中A,B為要相加的數，Cin為進位輸入；S為和，Co是進位輸出；

如果要實現多位加法可以進行級聯，就是串起來使用；比如32位+32位，就需要32個全加器；這種級聯就是串列結構速度慢，如果要並行快速相加可以用超前進位加法，

超前進位加法前查閱相關資料；

如果將全加器的輸入置換成A和B的組合函式Xi和Y（S0…S3控制）,然後再將X,Y和進位數通過全加器進行全加，就是ALU的邏輯結構結構。

即 X=f（A，B)

Y=f（A，B）

不同的控制參數可以得到不同的組合函式,因而能夠實現多種算術運算和邏輯運算。