數字邏輯
正文
主要用以研究有兩個離散狀態的開關器件所構成的數字電路。能對電路的輸入與輸出之間的關係提供理想描述,研究這種描述的特性和電路的實現,並探討將數字電路或數字模組互連起來完成特定邏輯功能的理論和方法。具有兩個或多個離散狀態的開關器件或單元是:可斷開和閉合的開關或繼電器的觸點;能正偏和反偏的整流二極體;能飽和和截止的開關電子管或開關電晶體;能在兩個飽和方向中任意一個方向上磁化的磁心。具有二個離散狀態的開關器件是最常見的。數字邏輯不考慮特殊條件下動作或穩定的物理現象和從一個狀態過渡到另一個狀態的細節。數字邏輯的部分理論建立在數理邏輯,特別是布爾代數和時序機的理論基礎上。
數字邏輯可分為組合邏輯和時序邏輯。在一個邏輯系統中,輸出結果僅取決於當前各輸入值的稱組合邏輯;輸出結果既由當前各輸入值,又由過去的輸入值來決定的稱時序邏輯。組合邏輯不包含存儲元件,時序邏輯至少包含一個存儲元件。
數字邏輯的套用範圍極廣,日常生活的決策過程是組合邏輯的典型例子。電話號碼的撥號和號碼鎖的開啟過程,則是時序邏輯的典型例子。數字邏輯在數字電路設計中有廣泛的用途。
組合邏輯 組合邏輯的輸出由其輸入確定的法則,通常稱為開關函式。因為變數是離散的,一個開關函式可以用表格形式的真值表來表示,也可以用各種圖來表示。如果函式和變數是二進制的,符號“1”和“0”通常用來表示這兩個值。這樣的函式能用二元布爾代數表達式來描述,稱開關函式。開關函式的二個數值,可以對應開和關,或繼電器觸點的閉合和開啟;可以對應電子電路電壓的高與低,或正和負;也可以對應邏輯真和假。
最簡單的開關函式是“非“函式、“與“函式和“或“函式。“非”函式表示為布爾非:Y=
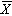 ,意即X為假,Y為真。“與”函式表示為布爾乘:Z=X·Y,意即僅當X·Y皆真,Z才真。“或”函式表示為布爾加:Z=X +Y,意即X或Y中任意一個為真,Z即為真。若用“1”表示邏輯“真”,“0”表示邏輯“假”,上述三個基本開關函式符合如下布爾代數法則:
,意即X為假,Y為真。“與”函式表示為布爾乘:Z=X·Y,意即僅當X·Y皆真,Z才真。“或”函式表示為布爾加:Z=X +Y,意即X或Y中任意一個為真,Z即為真。若用“1”表示邏輯“真”,“0”表示邏輯“假”,上述三個基本開關函式符合如下布爾代數法則: 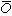 =10·0=00+0=0
=10·0=00+0=0 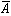 =00·1=00+1=1
=00·1=00+1=1 1·0=0 1+0=1
1·1=0 1+1=1
將這些基本邏輯單元加以組合,可以構成其他所有組合邏輯。這種邏輯可以根據輸入變數的真、假組合來確定輸出的真、假。因此,組合邏輯是一種決策邏輯,它可能十分簡單,也可能異常複雜。這些決策是需要某些邏輯數學方面的知識,也需要使用某些工具,如真值表、布爾代數、符號邏輯和波形等。
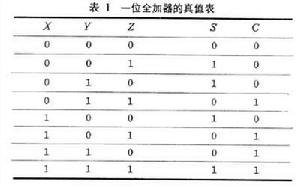
真值表 這是用真、假值來表示輸入邏輯變數與輸出開關函式之間關係的表格。它由兩部分組成,左邊一欄羅列輸入變數的各種可能取值,一般按大小順序排列。右邊一欄是與各輸入變數取值相對應的函式取值。表1是一位全加器的真值表。X、Y、Z分別表示加數、被加數和低位的進位。S 和C分別表示和以及本位進位。
 數字邏輯
數字邏輯S=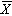 ·
·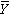 ·Z+
·Z+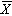 ·Y·
·Y·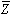 +X·
+X·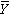 ·
·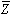 +X·Y·Z(1)
+X·Y·Z(1)
C=X·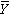 ·Z+X·Y·
·Z+X·Y·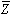 +X·Y·Z+
+X·Y·Z+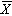 ·Y·Z (2)
·Y·Z (2)
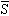 =(
=(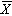 +
+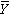 +
+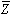 )·(
)·(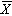 +Y+Z)·(X+
+Y+Z)·(X+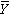 +Z)·(X+Y+
+Z)·(X+Y+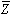 ) (3)
) (3)
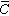 =(
=(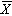 +
+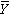 +
+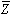 )·(
)·(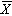 +
+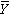 +
+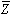 )·(
)·(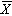 +Y+
+Y+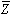 )·(X+
)·(X+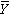 +
+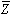 ) (4)
) (4)
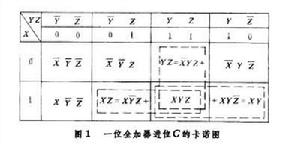
卡諾圖 卡諾圖是一種平面方格圖,每個方格代表標準函式中的一個最小項。方格的布局是按相鄰項和的對摺原理安排的,能清楚地表現其相鄰關係。卡諾圖是利用這種相鄰關係,合併最小項消去一些項來化簡函式的。圖1是式(2)三個變數的卡諾圖。
 數字邏輯
數字邏輯C=XY+XZ+YZ(5)
利用卡諾圖的方法可以化簡具有1個輸出和多到6個輸入的函式。當輸入變數增多時,函式可能的組合將非線性地迅速增長。另一方面,隨著微電子技術的發展,邏輯的規整性具有更重要的意義,因而函式最佳化的目標也有所改變。
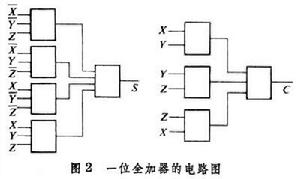
圖2是根據式(1)、(5)繪出的一位全加器的“與”“或”門電路圖。
 數字邏輯
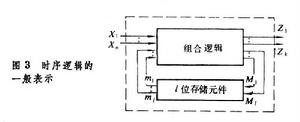
數字邏輯時序邏輯可表示為有反饋的組合邏輯,圖3是時序邏輯的一般表示。其中: xi、zi、Mj和mj
分別稱為輸入變數、輸出變數、狀態變數和次態變數。對時序邏輯,需要用兩組方程才能完整地描述其特性:
 數字邏輯
數字邏輯i=1,2,…,k
mj=fj(x1,…,xn,M1,…,Ml) (7)
j=1,2,…,l
關係式(6)表示,每個輸出變數 zi是當前輸入變數和狀態變數的布爾函式gi,gi稱為輸出函式。關係式(7)表示,次態變數(即下一個時刻的狀態變數)。可由當前輸入和狀態作自變數的布爾函式fj計算出來,fj稱為轉換函式。對時序邏輯,這些變數值通常在一些不連續的瞬間取樣。在進行下一次計算前,次態變數被存入存儲元件,作為新的狀態變數。
分類 用一個專門的定時信號作輸入(稱為“時鐘“)對狀態變數進行瞬間取樣來控制時序邏輯電路的動作,稱為“同步“時序電路。沒有專門定時信號的,稱為“異步”時序電路。同步時序電路的每個狀態都是穩定態,只有異步時序邏輯才有不穩定態。
競爭與冒險 以上論述的都是輸入和輸出穩定狀態之間的理想關係,沒有考慮電路實現中信號經過電路和導線的延遲和延遲時間的不均勻性。實際上,僅考慮理想的穩態解是不夠的,還必須研究過渡過程或暫態解。在數字邏輯電路的設計中常用競爭和冒險來分析過渡過程。所謂競爭,是指電路在瞬態過程中存在著一個以上的不穩定狀態變數。若電路所趨向的最終穩定狀態與狀態變數的變化次序有關,則稱電路的競爭是臨界的。否則,電路的競爭是非臨界的。臨界競爭會使電路的輸出結果不確定。為了消除競爭,可以在組合電路中插入可控制的延遲,或者通過適當的狀態賦值來消除臨界競爭。
冒險在組合電路和時序電路中都可能發生,但只對時序電路有嚴重影響。在一對相鄰輸入狀態的轉換過程中,可能導致電路的瞬間錯誤輸出,這種轉換過程稱冒險。為了消除冒險,可在次態變數的反饋環路中插入延遲單元,使輸入變數的變化完成後,再使狀態變數發生變化。
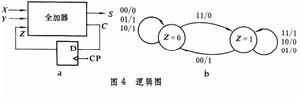
狀態表和狀態圖 正如組合邏輯可用真值表、函式式和卡諾圖等幾種形式來表示,時序邏輯可用狀態表和狀態圖來描述。狀態圖通常由狀態表推出,更直觀易讀,一般作為時序邏輯的原始設計規範。狀態圖用圓表示一個狀態,圓中的二進制數字表示這個圓所處的狀態。用連線圓的有向線表示狀態間的轉換。有向線上有兩個二進制數字,用“1”線割開,前者表示導致狀態轉換的輸入條件,後者指當前狀態下的輸出值。連線同一個圓的有向線表示狀態不變。狀態圖和狀態表提供同樣信息。圖4a是一個帶有一位全加器的邏輯圖,圖4b和表2是它的狀態圖和狀態表。
 數字邏輯
數字邏輯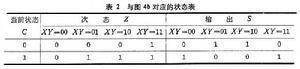 數字邏輯
數字邏輯Raymond E.Miller,Switching Theory,Wiley, New York,1979.
Samuel C.Lee,Modern Switching Theory and Digital Design,Prentice Hall, Englewood Cliffs,New Jersey.,1978.
Fredrick J. Hill,and Gerald R.Peterson,Introduction to Switching Theory and logical Design,2nd ed.,Wiley,New York,1974.
![數字邏輯[基於二進制數學或布爾代數的邏輯] 數字邏輯[基於二進制數學或布爾代數的邏輯]](/img/d/ad2/nBnauM3X0ADMzYTN0gTOzIzM2MTM5cTMxMDMwADMwAjMxAzL4kzL4IzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg)
