概念
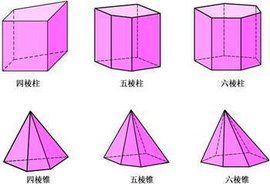
 立體圖形
立體圖形所有點不在同一平面上的圖形叫立體圖形。
對現實物體認識上的一種抽象,即把現實的物體在只考慮其形狀和大小,而忽略其它因素的基礎上在平面上的表示。
常用公式
 立體圖形
立體圖形長方體的表面積=2×(長×寬+長×高+寬×高) 用符號表示是:S=2(ab+bc+ca)
長方體的體積 =長×寬×高 用符號表示是:V=abc 或底面積×高 用符號表示是:V=Sh
正方體的表面積=棱長×棱長×6 用符號表示是:S=a²×6
正方體的體積=棱長×棱長×棱長 用符號表示是:V=a³
圓柱的側面積=底面周長×高 用符號表示是:S側=πd×h
圓柱的表面積=2×底面積+側面積 用符號表示是:S=πr²×2+dπh
圓柱的體積=底面積×高 用符號表示是:V=πr²×h
圓錐的體積=底面積×高÷3 用符號表示是:V=πr²×h÷3
圓錐側面積=1/2*母線長*底面周長
圓台體積=[S+S′+√(SS′)]h÷3
球體體積=(1/3*S*h)*(4*pi*R²)/S=4/3*pi*R²
特點
正方體
 立體圖形
立體圖形有8個頂點,6個面。每個面面積相等(或每個面都由正方形組成)。有12條棱,每條棱長的長度都相等。(正方體是特殊的長方體)
長方體
有8個頂點,6個面。每個面都由長方形或相對的一組正方形組成。有12條棱,相對的4條棱的棱長相等。
圓柱
上下兩個面為大小相同的圓形。有一個曲面叫側面。展開後為長方形或正方形或平行四邊形。有無數條高,這些高的長度都相等。
圓錐
有1個頂點,1個曲面,一個底面。展開後為扇形。只有1條高。
四面體有1個頂點,四面六條棱高。
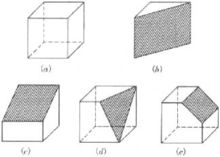
直三稜柱
三條側棱切平行,上表面和下表面是平行且全等的三角形。
主要作用
認識立體圖形,建立空間觀念。利用它們可以幫助學生直觀地認識各種物體的形狀和特點,自己動手擺出不同形狀的立體組合,還可以通過拆分體會各種幾何體之間的變換關係,從而加深對立體圖形特徵的認識和理解。 例如:兩個正方體可以組成一個長方體,一個圓柱體可以拆成兩個圓柱體。