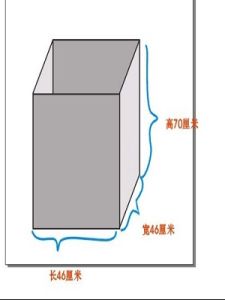
各部分名稱
長方體的每一個矩形都叫做長方體的面,面與面相交的線叫做長方體的棱,三條棱相交的點叫做長方體的頂點,相交於一個頂點的三條棱的長度分別叫做長方體的長、寬、高。底面是矩形的直平行六面體。長方體中,交於同一個頂點的三條棱的長度,分別稱為長方體的長、寬、高,合稱為三度。長方體的三度的平方和,等於它的對角線的平方。長方體的體積等於其長、寬、高的積。
特點
〔1〕長方體有6個面,每個面都是長方形,至少有兩個相對的兩個面完全相同。特殊情況時有兩個面是正方形,其他四個面都是長方形,並且完全相同。〔2〕長方體有12條棱,相對的棱長度相等。可分為三組,每一組有4條棱。還可分為四組,每一組有3條棱。〔3〕長方體有8個頂點。(4)長方體相鄰的兩條棱互相(相互)垂直。
體積
長方體的體積=長×寬×高。設一個長方體的長、寬、高分別為a、b、c,則它的體積V:V=abc=Sh因為長方體也屬於稜柱的一種,所以稜柱的體積計算公式它也同樣適用,長方體體積=底面積×高,V=Sh。這裡的S是底面積。關於長方體的體積公式,寫成V=abh是錯誤的。雖然字母h的確表示高(height),但是,如果用h表示高,那么長應該表示為l(length),寬應該表示為w(width),因此該公式表示為V=lwh,但如果用a表示長,b表示寬的話,就理所應當用c表示高了。而且,如果用了h,那s和e上哪去了?所以,長方體體積公式可以寫為V=abc、V=lwh或V=seh,但寫成V=abh是錯誤的,屬於不倫不類。
表面積
因為相對的2個面相等,所以先算上下兩個面,再算前後兩個面,最後算左右兩個面。設一個長方體的長、寬、高分別為a、b、c,則它的表面積S:S=2ab+2bc+2ca=2(ab+bc+ca)
棱長
長方體的棱長之和=(長+寬+高)×4長方體棱長字母公式C=4(a+b+c)相對的棱長長度相等長方體棱長分為3組,每組4條棱。每一組的棱長度相等。
對角線長
長方體的對角線是長方體的任意一個頂點到對邊頂點的長度,對角線的長度:依據勾股定理,點2和點3的長度是根號(點1到點2的長度的平方+點1到點3的長度的平方),而點2到點3的線又與點3到點5的長度形成直角,所以對角線的長度是:註:(x,y)是指點x到點y的長度。