相關比較
與三角形中位線作對比
| | 三角形 | 梯形 |
| 中位線概念 | 連結三角形兩邊中點的線段叫做三角形的中位線． | 連結梯形兩腰中點的線段叫做梯形的中位線。 |
| 要點 | 連結三角形兩邊中點的線段而不是連結一頂點和它的對邊中點的線段 | 連結兩腰中點的線段而不是連結兩底中點的線段。 |
| 聯繫 | 三角形可看成上底為零的梯形，則梯形的中位線成三角形的中位線 | |
| 中位線定理 | 三角形的中位線平行於第三邊並且等於它的一半 | 梯形的中位線平行於兩底，並且等於兩底和的一半。 |
定理證明
如圖1梯形ABCD，E為AB的中點，F為CD的中點，連線EF，
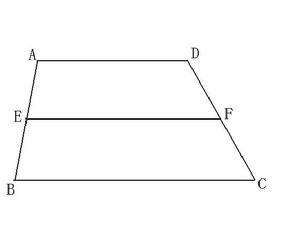梯形中位線證明圖求證：EF平行兩底且等於兩底和的一半。
證明：連結AF，並延長AF於BC延長線交於點O
在△ADF和△FCO中
∵ AD//BC
∴ ∠D=∠1 圖1
又∵ ∠2=∠3 DF=CF
∴ △ADF≌△FCO
∵ 點E,F分別是AB，AO中點
∴ EF為三角形ABO中位線
∴ EF∥OB即EF∥BC
∵ AD//BC
∴ EF∥BC∥AD（EF平行兩底）
∵ EF為三角形ABO的中位線
∴ 2EF=OB
OB=BC+CO CO=AD
∴ 2EF=BC+AD
∴ EF=（BC+AD）÷2（EF等於兩底和的一半）
梯形的中位線平行於上下兩底且等於兩底和的一半
