lipschitz條件

在數學中，特別是實分析，lipschitz條件，即利普希茨連續條件（Lipschitz continuity），以德國數學家魯道夫·利普希茨命名，是一個比通常連續更強的光滑性條件。直覺上，利普希茨連續函式限制了函式改變的速度，符合利普希茨條件的函式的斜率，必小於一個稱為利普希茨常數的實數（該常數依函式而定）。 在微分方程，利普希茨連續是皮卡-林德洛夫定理中確保了初值問題存在唯一解的核心條件。一種特殊的利普希茨連續，稱為壓縮套用於巴拿赫不動點定理。 利普希茨連續可以定義在度量空間上以及賦范向量空間上；利普希茨連續的一種推廣稱為赫爾德連續。

定義

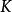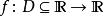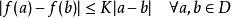lipschitz條件

lipschitz條件

lipschitz條件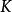

lipschitz條件

lipschitz條件

lipschitz條件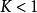

lipschitz條件

lipschitz條件

lipschitz條件

對於在實數集的子集的函式，若存在常數，使得，則稱符合利普希茨條件，對於最小的常數稱為的 利普希茨常數。若，稱為收縮映射。

利普希茨條件也可對任意度量空間的函式定義：

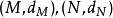lipschitz條件

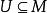lipschitz條件

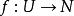lipschitz條件

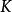lipschitz條件

給定兩個度量空間，。若對於函式，存在常數使得

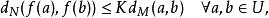lipschitz條件

則說它符合利普希茨條件。

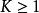lipschitz條件

若存在使得

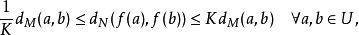lipschitz條件

lipschitz條件

則稱為 雙李普希茨(bi-Lipschitz)的。

皮卡-林德洛夫定理

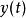lipschitz條件

lipschitz條件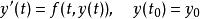

lipschitz條件

若已知有界，符合利普希茨條件，則微分方程初值問題剛好有一個解。

lipschitz條件

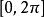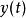lipschitz條件

lipschitz條件

lipschitz條件

在套用上，通常屬於一有界閉區間（如）。於是必有界，故有唯一解。

例子

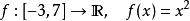lipschitz條件

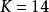lipschitz條件

符合利普希茨條件，。

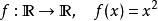lipschitz條件

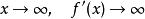lipschitz條件

不符合利普希茨條件，當。

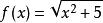lipschitz條件

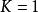lipschitz條件

定義在所有實數值的符合利普希茨條件，。

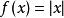lipschitz條件

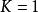lipschitz條件

符合利普希茨條件，。由此可見符合利普希茨條件的函式未必可微。

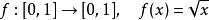lipschitz條件

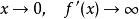lipschitz條件

不符合利普希茨條件，。不過，它符合赫爾德條件。

lipschitz條件

若且唯若處處可微函式f的一次導函式有界，f符利普希茨條件。這是中值定理的結果。所有函式都是局部利普希茨的，因為局部緊緻空間的連續函式必定有界。

性質

符合利普希茨條件的函式一致連續，也連續。

bi-Lipschitz函式是單射的。

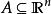lipschitz條件

lipschitz條件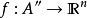

lipschitz條件

Rademacher定理：若且為開集，符利普希茨條件，則f幾乎處處可微。

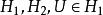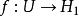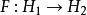lipschitz條件

lipschitz條件

lipschitz條件

lipschitz條件

lipschitz條件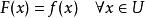

lipschitz條件

Kirszbraun定理：給定兩個希爾伯特空間，符合利普希茨條件，則存在符合利普希茨條件的，使得的利普希茨常數和的相同，且。