簡介
Williams-Landel-Ferry方程(簡稱WLF方程)是高分子物理中一個非常重要的經驗公式。其中, C1 、C2 作為兩個經驗參數， 取決於參考溫度Tr 的取值， 且其乘積為定值(C1·C2 ≈ 900)， 與自由體積熱膨脹係數αf有關。藉助於WLF方程的變形式C1 、C2 參數有兩種不同求解方法，與由-1/ logαT 對1/(T-Tr)作圖的方法I相比較， 由-(T -Tr)/ logαT 對(T -Tr)作圖的方法II的靈敏度更高， 平均相對殘差更小，由於對(T -Tr)變化的更高的敏感回響， 導致方法II 作圖的線性相關性(相關係數)較低 。
WLF方程的推導及意義
對許多非晶態聚合物，通過把在不同溫度下得到的幾個不同時間數量級的實驗模量～溫度曲線水平位移，可以疊合成一條主曲線。在時間軸上的水平位移α符合以下關係
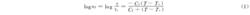（1）α位移因子，τ和τ分別為溫度在T、Tr時的鬆弛時間，C、C經驗參數，Tr為參考溫度。根據位移因子α的定義，有
（2）ρ、ρ分別為溫度為T、Tr時的密度，η、ηr分別是溫度為T、Tr時的粘度。
在實驗溫度範圍內，聚合物的密度變化很小，且溫度取絕對溫標，意味著T大即ρ小，Tr小則ρr大，故(ρrTr/ρT)可近似取1，則
（3）故α就可轉化為不同溫度下的粘度比。
根據自由體積理論，某溫度下高聚物的實際體積V等於高分子本身固有的體積V及自由體積V之和。液體粘度與本身的自由體積相關，其關係
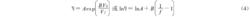（4）A、B 為常數，f為自由體積分數V/V。實驗結果表明，對幾乎所有材料而言，B ≈1。
自由體積分數同溫度的關係
（5）fr為參考溫度Tr時的自由體積分數，α為自由體積熱膨脹係數。
由式(4)和式(5)可得
（6）比較式(6)與式(1)，可得WLF方程中的C、C
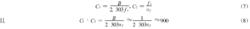（7）（8）即C1·C2為定值，與α有關。當選擇玻璃化溫度Tg作為參考溫度時，C和C具有近似的普適值(大量實驗值的平均值):C=17.44，C=51.6。因此，可求得在玻璃化溫度Tg下的自由體積分數fg=0.025，α=4.8×10/K。
WLF 方程重要的意義在於， 低溫下測定的力學數據就可換成短時(或高頻)下的數據;另一方面高溫測定的力學數據可轉換為長時(或低頻)下的數據 。
C1、C2參數的意義
作為兩個經驗參數，式(1)中C、C取決於參考溫度Tr的取值。由式(7)可知，當認同B≈1，則C與參考溫度Tr下的自由體積分數fr有關，是一個無量綱的參數;而C不僅與參考溫度Tr下的fr有關，還與α有關，且量綱為K。
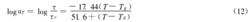（12）當選擇Tg作為參考溫度時，由大量實驗結果的平均值得到C=17.44，C=51.6，則相應的WLF方程
除Tg外，對所有高聚物均還可以找到一個對應的特徵參考溫度Ts。此時，可得到對應的另一組參數:C=8.86，C=101.6。當選擇Ts作為參考溫度時，WLF方程為
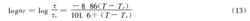（13）式中，Ts 因聚合物不同而異 。
