基本資料
基本資料姓名：蔡四維
職業：教授
籍貫：湖南益陽人
1927年2月16日 出生於湖南省益陽市。
1949年 畢業於中央大學（今南京大學）。
1949-1950年 任鐵道兵團第三橋樑大隊技術員。
1950-1962年 任水利部治淮委員會工程師。
1962-1970年 任安徽水利電力學院教員。
1970年- 任合肥工業大學教授。
2012年8月24日在合肥逝世。
生平簡介
家庭背景
蔡四維，1927年2月16日出生於湖南省益陽市。抗日戰爭初起，他進入國中學習，學校位於益陽的一個偏僻鄉村，畢業後考入湖南長郡高中，該校也坐落於湖南中部的一個小鎮。每年寒暑假回家，他均需負笈步行三百餘里。由於親見中國交通不便所帶來的民生窮困，自此他立志將來從事國家道路橋樑建設工作。
成績優異
中學求學期間，他學習刻苦，各科成績俱佳。高中畢業時，抗日戰爭雖已接近尾聲，但湘北大部分地區已經淪陷，他乃邀約同學數人，迂迴取道來到重慶，考入中央大學土木系學工程結構專業。次年隨學校遷回南京就讀，於1949年7月畢業。此時學校易名南京大學。
報效祖國
中華人民共和國成立，土木工程事業百廢俱興。為回響黨和國家的號召，蔡四維積極投身到祖國建設第一線，希望用自己所掌握的知識報效祖國。
1949年，在他擔任鐵道兵團第三橋樑大隊技術員半年的時間裡，他參加修復隴海路洛河橋及湘桂路衡陽橋兩項工程，支援解放祖國的西南部。由此，他也積累了許多工程實踐知識。
治淮工作
1950年轉入治淮工作，當年他參加了蘇北一項被日本侵略軍破壞了的船閘修復工程。這項工程原設計是外國工程師做的，當他認真研究後，發現原設計理論有盲目性，材料浪費，施工不便，存在諸多問題。經過實地調查和仔細分析，蔡四維大膽地提出了自己的見解，並從此開展了他在廣泛工程範圍內對土木結構、地基基礎、滲流、水流、彈性地基等方面的鑽研。
研究工作
自1950年至1962年這12年中，蔡四維一直擔任水利部治淮委員會工程師，這是他初期的研究工作階段。當時既無導師指點，資料、情報的索取也不能得心應手，更加上設計任務不斷，工地往返流動極大，在這樣的條件下，蔡四維本著自強的心理，克服困難，突破工程技術上的難關，他幾乎將所有的業餘和節假日時間都用於學習和研究，翻閱了大量的國內外有關資料，終於解決了很多工程上亟待解決的問題。
學院任教
1962年，蔡四維被調到安徽省水利電力學院任教，1970 年又隨該學院合併至合肥工業大學任教，講授水工結構、結構力學、彈性力學等課程。在完成繁重教學任務的同時，他總是繼續堅持著科學研究工作。即使在60年代末“文化大革命”時期，蔡四維出自對科學的熱愛和追求，學習鑽研堅持不懈。當他了解到關於結構力學有限元方面的研究在國外已很盛行時，他立即認識到計算機套用、矩陣方法、有限元是工程結構分析的極有用的工具方法，應該急起直追，並自己著手研究起來。然而，在當時的環境下看書學習的機會極少，為了抓緊時間，他將好不容易才弄到手的書刊資料拆成活頁帶在身邊，便於在“勞動鍛鍊”之餘能讀上幾頁。他堅信他的研究對國家建設有用，後來，他這方面的研究成果終於得到了出版，受到國內外同行學者們的好評。
1976年，祖國迎來了新的春天。和全國的知識分子一樣，蔡四維受到了黨和國家的關懷。1978年他被評為合肥工業大學的力學教授，安徽省給他以先進科技工作者的榮譽稱號，他光榮地出席了該年在北京召開的全國科學代表大會。
結構力學
70年代他參加了中國科學院受控核聚變裝置的研製工作，因而接觸到新的複合材料，並認識到複合材料的優越性能和廣泛的工程套用價值。從此，蔡四維便開始了複合材料結構力學方面的研究。之後，從連續纖維複合材料到短纖維複合材料，從纖維加強塑膠到纖維加強混凝土，凡是國際上有關研究的熱點，凡是工程實踐中迫切需要的內容，他都刻苦鑽研，兢兢業業。歷年來取得並在國內外發表了他的研究成果。
在高校任教30餘年，蔡四維為國家培養了大批的建設人才。他教書育人，對年輕教師和學生既熱心幫助，又嚴格要求。他的嚴謹治學、為人師表，深受人們的敬重。如今蔡四維雖已古稀之年，但仍然保持著旺盛的精力，正帶領著他的研究小組成員進行著短纖維複合材料的力學性能研究和推廣它在土木工程上的套用，為既能培養人才又能提出科研成果而奮鬥不止。
科技成就
自1949年到1962年，蔡四維在土木工程建設第一線從事工程設計與施工工作。當時工程上存在著大量亟待解決的問題。在繁忙工作的同時，他利用業餘時間選擇了有關的課題進行刻苦鑽研，在《工程建設》、《土木工程》、《水力發電》、《水電技術》、《土木工程學報》等期刊上發表文章。其研究特點主要是從工程實際出發，提出具有充分理論依據而又極便於工程師套用的方法，取得了一定的經濟效益和社會效益。
地基基礎
1949年以前，水工建築物一般都採用樁基礎，50年代蘇聯專家來我國推薦無樁基礎，當時工程單位為了解“地基允許承載能力”而進行現場荷載試驗，蔡四維指出，水工建築荷載面大且分布複雜，這使地基的較大範圍和深度受到影響，小面積的承載能力試驗不能反映這些實際情況。為此他認為這種試驗工作耗費大而無實用價值，並指出水工建築地基承載能力應結合地基沉陷與建築物適應性來決定，他的這種觀點後來在1953年初《工程建設》35期上發表。他並針對水工建築物荷載分布的特點，根據半無限體彈性理論的J·布希涅斯克（BousSinesq）解導出了用圖解很快求得地基任意深度和範圍內應力分布的方法，供工程師們用來計算地基應力，估算地基沉陷，以作為基礎設計的依據。這部分內容後來在1957年的《土木工程》上發表。
地基應力
關於相鄰建築物對地基應力影響的研究
緣自於1954 年蚌埠市自來水廠因新水池建成後造成近旁原有水池開裂。當時，合肥市組織專家進行事故審查，蔡四維也受邀前往，各地到會老專家甚多，大都指責舊池設計上的缺點，蔡四維則力排眾議，提出該事故原因是新池荷載造成舊池地基不均勻附加應力而引起舊池不均勻沉陷開裂。他並提出對舊池的修復建議。他的論點最後為到會專家一致稱讚並被採納。自此他對鄰近建築物間地基應力的相互影響極為重視。50年代，彈性地基梁計算在工程上很多採用錢令希教授的級數解法（見《土木工程學報》1954），蔡四維在錢公式上附加鄰近荷載影響的內容，所提出的公式、方法於50年代後期在安徽阜陽地區水閘工程設計上普遍採用而行之有效。爾後在他自己的彈性地基梁解法中，亦引用了鄰近建築影響的分析計算。
水工建築物
砂性基礎上的水工建築物研究 對建造在砂性基礎上的水工建築物設計，基礎滲流問題是一個重點。滲流除造成建築物受浮托力外，滲流坡降、特別是滲流逸出坡降也極其重要。當時印度A.N.柯斯拉、（Khosla）提出的砂基滲流問題的分析計算方法只適應於無限深層砂基礎，實際工程中很多是有限滲水層基礎。蔡四維考慮到有限滲水層上閘基地下輪廓設計的需要，最初引進並介紹了H.H.巴甫洛夫斯基（ЛавоΛовсиии）的解法，之後他又根據複變函數的共形寫象法將實際滲流區進行轉換，最後利用巴甫洛夫斯基的成果提出了一種簡單的解法，這些成果後來發表在《工程建設》（1956）、《水利水電技術》（1963）上。
水力沖填築壩的研究 50年代國外已有水力沖填興築土壩土堤的研究，我國為取得自己國家的研究經驗，水利部於1956年在淮河上建立現場實驗，蔡四維參加了這項工作。在此期間他提出水力沖填壩穩定分析方法和壩身滲透理論研究成果。水力沖填壩自然形成為心牆式，心牆土顆粒細，排水慢，長期處於塑流狀態，他即從心牆塑流狀態出發分別提出壩身和壩身連同地基的穩定分析法，此外，又從達西（Dacy）定律出發導出了滲流計算公式。這部分成果後來發表在《水力發電》（1957）上。
涵洞水力學
涵洞管道水力學計算 過去的計算方法大都根據涵洞上下游水頭落差、涵洞面積計算流量或根據流量設計涵洞面積。蔡四維認為已有常用方法不盡合理，他提出應根據涵洞泄水面積、水流進出口形式、洞身長短、坡降緩急等諸多因素來合理地進行設計計算，並闡述了涵洞水流的各種流態，撰寫《涵洞孔徑流量》一文在《工程建設》（1956）上發表。
上述幾個方面的研究成果發表後，蔡四維先後收到了很多工程師邀請協助解決工程技術問題的信函，他提出的方法在工程上得到廣泛套用，這使他受到了很大的鼓舞和促進，同時也促使他向更新、更深的研究領域探索。
彈性地基梁
彈性地基梁的研究
1962年後，他被調去高校任教，為配合教學工作需要，自此就專攻結構力學。
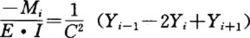梁的基本方程式過去我國對彈性地基梁的分析，僅限於採用文克爾（Winker）理論。到了50年代後期，由於國家大規模經濟建設的需要，同時半無限體理論的優越性逐漸為工程上所認識，有必要去研究一種更為合理有效的計算彈性地基梁的方法。當時在中國科學院學部委員錢令希教授的帶領下，工程界出現了一個開展這項研究工作的熱潮。受錢令希教授的論著及研究成果的啟發，蔡四維研究並提出了一種解彈性地基梁的新方法，在《中國科學》（1961）、《土木工程學報》（1959 年）上發表，並寫成《彈性地基梁》一書，由上海科技出版社於1962年出版。當時工程界對其研究成果非常重視，譽之為“蔡氏法”。該方法在工程上得到了廣泛的套用。中國科學院1959年編《十年來的中國科學》一書給“蔡氏法”以高度的評價稱：“最近提出了一個效果很好的方法，就是用差分形式寫出梁的基本方程式：式中Yi是梁的撓度，由於連續條件，它等於地基面的沉陷值，為未知反力Pk的函式。根據分段數目n，把方程式的右部用彈性力學公式列為Pk（k=1，2，…，n）的現成表達式，方程式左邊的Mi是i截面的撓矩，是外荷載和反力Pk的函式，可以直接寫出來，於是十分簡便地可以列n-1個必要的方程式，再加上2個平衡方程式∑Y=0和∑M=0，就完成了建立方程式的工作。方程式的數目為n+1，比日莫契金的方法要少兩個，而寫出這些方程式的工作可以說比目前任何方法要簡捷得多，還有一點值得注意，就是這一方法可以很容易地處理變截面地基梁問題。”此外，著名科學家、中國科學院學部委員潘家錚教授，在他所著《彈性地基上的梁和框架》一書綜合評述已有各種方法時稱：“蔡氏法…與以前各法有很大不同，…蔡氏建議的途徑…是很巧妙的一步，…而且大部分工作可事先編製成表，以供實際檢用，從而使計算工作簡化。蔡氏法確為解彈性地基梁基本方程式的一種新穎有效的方法。”“能夠簡化方程組的建立解算工作，因此具有很大的價值。”
從近代計算技術的角度來看，蔡氏法仍有其獨特的優點，便於在計算機上工作，美國Viginia州立大學C.S.迪塞（Desai）教授等近年來出版的《工程數值方法》專著中，再次推薦並轉載了“蔡氏法”。
有限元方法
結構矩陣方法及有限元方法的研究60年代後期，蔡四維了解到國際上已大量開展結構力學矩陣方法和有限元方法的研究與套用，他認為這類方法配合計算機套用是結構力學分析的極有成效的方法，有著廣闊的套用前景。他在信息閉塞、資料缺乏、無計算機設備的困難條件下，依靠獨自摸索，開展了這方面的研究工作。
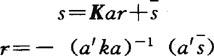公式國外桿繫結構矩陣方法中，有一種按結點彎矩平衡建立方程而後疊代求解的方法，他們用結點各桿近端彎矩為未知量，隨結點和桿數增多，方程階數增高。蔡四維提出改用結點各桿近端彎矩之和為未知量，方程組階數就大大減少了，最後通過各結點近端彎矩之和進行簡單的分配即可得到各桿近端彎矩。這一方法使計算工作量大為減少而精度卻不變。 國外位移法矩陣分析中，從下列公式 ：出發，結點位移r元素增多時，勁度矩陣k階數增高，求（a′ka）-1工作量。蔡四維提出將a的各列陣a1，a2，a3，…與r各元素拆開即令，然後消去r1，並逐次進行，他導出了k（1），k（2）…k（m-1），，…+，為此極易求得rm，rm-1，rm-2…r3，r2，r1。因為在使用這一方法時，每一步都可以同時消去多個r元，故他稱之為分塊疊代法。
矩陣轉移法是通過梁兩端參量（變位和端力）間的矩陣式連續替代，最後使連續梁最右端支點參量用最左端支點參量表達，並由兩端支承條件求解，此法的困難在於跨間荷載影響項的計入。為此，蔡四維提出將問題化為固定與放鬆兩態作迭加，用固定態跨間外載下支點不平衡彎矩作放鬆態的結點荷載，只須進行放鬆態的連續轉移後與固定態迭加求解，這樣使問題很大程度地簡化，同時他提出一些便於計算的圖表，套用極為方便。
上述幾個方面的研究成果均載入他的專著《結構力學矩陣方法》一書中，於1975年科學出版社出版，該書以後連印三次。
帶極薄夾層物體的有限元分析是針對核聚變托卡馬克裝置線圈分析而提出的方法，蔡四維用通常的四邊形單元在原有位移模式u=∑NiUi，υ=∑NiVi上分別附加NAUA+NBUB，NAVA+NBVB項，併合理選擇NA，NB的函式形式，使單元內應變很好地滿足具有夾層的特性，這樣取用的單元能推廣用於一單元內有多個夾層的情況，也可以退化為無夾層單元，實用上可取較大尺度的單元，得到精確的解。該項內容在1981年機械部召開的中國合肥有限元國際邀請學術報告會上報告並印發，後刊登在《合肥工業大學學報》
矩陣轉移法是通過梁兩端參量（變位和端力）間的矩陣式連續替代，最後使連續梁最右端支點參量用最左端支點參量表達，並由兩端支承條件求解，此法的困難在於跨間荷載影響項的計入。為此，蔡四維提出將問題化為固定與放鬆兩態作迭加，用固定態跨間外載下支點不平衡彎矩作放鬆態的結點荷載，只須進行放鬆態的連續轉移後與固定態迭加求解，這樣使問題很大程度地簡化，同時他提出一些便於計算的圖表，套用極為方便。
上述幾個方面的研究成果均載入他的專著《結構力學矩陣方法》一書中，於1975年科學出版社出版，該書以後連印三次。
帶極薄夾層物體的有限元分析是針對核聚變托卡馬克裝置線圈分析而提出的方法，蔡四維用通常的四邊形單元在原有位移模式u=∑NiUi，υ=∑NiVi上分別附加NAUA+NBUB，NAVA+NBVB項，併合理選擇NA，NB的函式形式，使單元內應變很好地滿足具有夾層的特性，這樣取用的單元能推廣用於一單元內有多個夾層的情況，也可以退化為無夾層單元，實用上可取較大尺度的單元，得到精確的解。該項內容在1981年機械部召開的中國合肥有限元國際邀請學術報告會上報告並印發，後刊登在《合肥工業大學學報》。
板殼結構力學
複合材料與多層粘合板殼結構力學研究
纖維複合材料結構，是以多層粘合成型的形式出現，其理論研究在國際上受到高度重視，論著極多。綜合近20年來的研究成果，大體上有兩種理論分析方法，即分層分析法與高階理論分析法。蔡四維對這兩種理論都提出了自己的新解法。在分層分析法方面，他提出以層間位移為基本未知量，考慮橫向剪下效應，在建立各層控制微分方程式之前，先引進層間應力平衡條件，最後由各層控制微分方程連同整體邊界條件求解。此法保證了在每一層內滿足全部彈性力學方程和整體各層間應力、位移連續條件以及整體邊界條件，因而是一種高精度的解析解法。經典的分層法是以各層中面位移和中面法線轉角（或層間剪下應力）為基本未知量，相比之下，蔡四維提出的方法中未知量總數要比經典方法少得多，這給分析計算帶來了很大的簡便。在高階分析法方面，蔡四維最初提出：設定橫斷面橫向剪應力分布，導出以兩個剪應力函式和一個中面撓度為未知數的控制方程。這種3個未知函式的方法，取得了與5個未知量（即中面位移和中面法線轉角為未知量）的經典方法同樣效果。但是由於經典法和他提出的方法其層間應力平衡或位移連續條件未能全部滿足，因而他不為此停步，進而又提出了在設定橫向剪應力分布時，引進海氏（Heaviside）函式，以保證滿足層間連續條件。其方法最後使控制微分方程只有5個，所得的結果與目前最高階的高階法具有相同的精度，而後者控制微分方程達9個之多。
以上成果先後在中國《力學學報》（1988），《複合材料學報》（1988、1989），第一屆國際複合材料會議（北京）（1986）以及英國《複合材料結構》（composite structure 4，6卷）等期刊或學術會議上發表，蔡四維在英國Nottingham 大學、Paisley大學等處講學，受到了海內外專家學者的關注。此外，對多層粘合梁、板結構承受集中荷載的情況，他提出用理論解與邊界配點相結合的方法求解著力點下應力集中問題。這一方法曾經英國諾丁漢（Nottingham）大學H.費斯勒（Fessler）教授等用實驗法驗證了其精確性。並就該內容著文載於第七屆國際複合材料會議文集。對複合材料其它有關研究還有如《纖維複合材料橫向荷載下應力集中》、《各向異性材料迭層層間裂紋尖端應力奇導性分析》等方面的內容，在中國《固體力學學報》（1982）、第七屆國際複合材料會議文集。此外，他還著有《複合材料結構力學》一書，於1988年人民出版社出版。該書已列入1990年出版的《中國優秀科技圖書要覽》中。
短纖維複合材料
短纖維複合材料的研究
80年代，蔡四維在英國諾丁漢大學工作期間，了解到短纖維複合材料有很多優點，例如它有較好的各向同性，便於自動化生產，成本較低等。他注意到對該材料的研究與套用近年國外已取得飛快進展，因此，1988年他回國後即開展這一方面的研究。研究工作得到了國家自然科學基金和有關部門的資助，除研究短纖維加強塑膠外，他並配合交通部門的需要，對短切鋼纖維加強混凝土用於路面這一課題，承擔了有關實驗與理論分析工作，其中部分研究成果，曾獲1991年及1993年安徽省及交通部科技進步獎。與此同時，蔡四維並提出用短纖維加強瀝青混凝土用作路面材料，在對這種材料的強度、韌性、裂紋擴展特性等進行了系統研究後，指出在路面一般使用溫度下，這種材料具有粘彈性特徵，且它可歸類於熱流變簡單材料，利用時溫等效性及WLF方程，從一個溫度下該材料的本構方程，即可求出不同溫度下的本構方程，同時他指出，同一溫度下應變率提高，和同一應變率下溫度降低，對該材料強度的變化有相同效果。為此指出可以從某一溫度下應變率與強度關係求出任意溫度和應變率下的材料強度。除從理論上闡述用纖維瀝青混凝土作路面的技術可行性和經濟合理性外，他和其合作者並在安徽境內築了一段實驗路面驗證了其理論，有關短纖維複合材料的研究成果，主要發表在第九屆國際複合材料會議論文集（1993）《複合材料進展》（航空工業出版社1994）和《複合材料學報》（1995）上。此外，蔡四維著《短纖維複合材料理論與套用》一書，已於1994年人民交通出版社出版。該書概括了他及其合作者幾年來的部分研究成果
主要論著
1 Cai Si-Wei. Solution of Beams on Elastic Foundations.中國科學,May 1961,Ⅹ(1):113～152.
2 蔡四維.彈性地基梁解法.上海：上海科學技術出版社，1962.
3 蔡四維.結構力學的矩陣方法.北京：科學出版社，1975.
4 蔡四維，蔡敏。有限元素法.北京：科學出版社，1980.
5 蔡四維.複合材料結構力學.北京：人民交通出版社，1987.
6 蔡四維.短纖維複合材料理論與套用.北京：人民交通出版社，1994.
7 Cai Si-Wei. A refined theory for laminated anisotropic cylindrical shell. Beijing, China:Proc. International Symposium on Composite Materials and Structure, June 1986:154—161,力學學報(中文版),1988,20(1):86～94.
8 Cai Si-Wei. A refined theory for laminated doubly curved shells.Composite Structure, UK. Elsevier Applied Science Press, 1987,1：262-274.複合材料學報，1989，（2）：15～23.
9 蔡敏，蔡四維.對稱層板的一種解法。複合材料學報，1988，5，（2）：97～100. 10 Cai Si-Wei.A refined theory for laminated anisotropic plates.Composite structure, UK, Elsevier Applied Science press, 1991,6,383～396.
