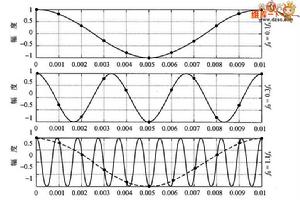
定理說明
採樣過程所應遵循的規律,又稱取樣定理、抽樣定理。採樣定理說明採樣頻率與信號頻譜之間的關係,是連續信號離散化的基本依據。
在進行模擬/數位訊號的轉換過程中,當採樣頻率fs.max大於信號中最高頻率fmax的2倍時(fs.max>2fmax),採樣之後的數位訊號完整地保留了原始信號中的信息,一般實際套用中保證採樣頻率為信號最高頻率的2.56~4倍;採樣定理又稱奈奎斯特定理。
如果對信號的其它約束是已知的,則當不滿足採樣率標準時,完美重建仍然是可能的。 在某些情況下(當不滿足採樣率標準時),利用附加的約束允許近似重建。 這些重建的保真度可以使用Bochner定理來驗證和量化。
歷史回顧
1924年奈奎斯特(Nyquist)推導出在理想低通信道的最高碼元傳輸速率的公式。
1928年美國電信工程師H.奈奎斯特推出採樣定理,因此稱為奈奎斯特採樣定理。
1933年由蘇聯工程師科捷利尼科夫首次用公式嚴格地表述這一定理,因此在蘇聯文獻中稱為科捷利尼科夫採樣定理。
1948年資訊理論的創始人C.E.香農對這一定理加以明確地說明並正式作為定理引用,因此在許多文獻中又稱為香農採樣定理。採樣定理有許多表述形式,但最基本的表述方式是時域採樣定理和頻域採樣定理。
採樣定理在數字式遙測系統、時分制遙測系統、信息處理、數字通信和採樣控制理論等領域得到廣泛的套用。
定理分類
時域
頻帶為 F的連續信號 f( t)可用一系列離散的採樣值 f( t1), f( t1±Δ t), f( t1±2Δ t),...來表示,只要這些採樣點的時間間隔Δ t≤1/(2 F),便可根據各採樣值完全恢復原來的信號 f( t)。 這是時域採樣定理的一種表述方式。
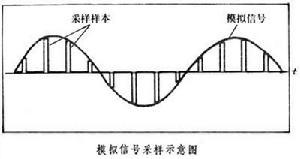
時域採樣定理的另一種表述方式是:當時間信號函式 f( t)的最高頻率分量為 fM時, f( t)的值可由一系列採樣間隔小於或等於1/(2 fM)的採樣值來確定,即採樣點的重複頻率 f≥(2 fM)。圖為模擬信號和採樣樣本的示意圖。
時域採樣定理是採樣誤差理論、隨機變數採樣理論和多變數採樣理論的基礎。
頻域
對於時間上受限制的連續信號 f( t)(即當│ t│> T時, f( t)=0,這裡 T= T2- T1是信號的持續時間),若其頻譜為 F( ω),則可在頻域上用一系列離散的採樣值 來表示,只要這些採樣點的頻率間隔ω≦π / tm 。
 採樣定理
採樣定理 採樣定理
採樣定理相關公式
 採樣定理
採樣定理理想低通信道的最高碼元傳輸速率B=2W Baud (其中W是頻寬)理想信道的極限信息速率(信道容量)。
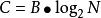 採樣定理
採樣定理( bps )
多變數信號和圖像的套用
 圖像套用
圖像套用採樣定理通常針對單個變數的函式進行公式化。因此,定理可直接適用於時間相關的信號,並且通常在該上下文中公式化。然而,採樣定理可以以直接的方式擴展到任意多個變數的函式。
灰度圖像通常表示為代表位於行和列採樣位置的交叉處的像素(圖像元素)的相對強度的實數的二維陣列(或矩陣)。因此,圖像需要兩個獨立變數或索引,以指定每個像素唯一一個用於行,一個用於列。
彩色圖像通常由三個單獨的灰度圖像的組合構成,一個代表三原色(紅色,綠色和藍色)或簡稱RGB中的每一個。對於顏色使用3向量的其他顏色空間包括HSV,CIELAB,XYZ等。諸如青色,品紅色,黃色和黑色(CMYK)的一些顏色空間可以通過四維表示顏色。所有這些都被處理為二維採樣域上的向量值函式。
類似於一維離散時間信號,如果採樣解析度或像素密度不足,圖像也可能遭受混疊。例如,具有高頻率(換句話說,條紋之間的距離小)的條紋襯衫的數碼照片可以在襯衫被照相機的圖像感測器採樣時導致襯衫的混淆。對於這種情況,在空間域中採樣的“解決方案”將是更靠近襯衫,使用更高解析度的感測器,或者在用感測器採集圖像之前對圖像進行光學處理。