簡介
一個金屬-絕緣層-半導體(MIS)結構是一片絕緣層被夾在金屬層和半導體層之間。並且,一個MIS結構的直流電導為零。半導體通常在背後有一個歐姆接觸。絕緣體通常選擇使用其半導體的氧化物。特別的,把二氧化矽做在矽表面上的工藝是非常先進成熟的,由這種氧化物工藝形成的結構,叫做MOS(Metal-oxide-Semiconductor)結構。而且這種結構極其重要,可以用來研究半導體表面、整合電子電路或者和用於CMOS(Complementary Metal Oxide Semiconductor/互補金屬氧化物半導體)技術,而且CCDs(charge-coupled devices/電荷耦合器件)也是基於這種MIS結構
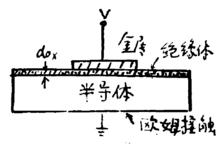 MIS結構
MIS結構理想的MIS結構/空間電荷層及表面勢
金屬一絕緣體一半導體結構(簡稱MIS結構),如圖所示。以氧化物(例如矽的氧化物Sioz)作為絕緣體,就叫MOS結構。MOS是構成電晶體的基本結構。在金屬端加正電壓(稱為控制極電壓)時,取作V>O。
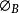 MIS結構
MIS結構圖中表示V=O時,n型/p型半導體的理想MIS結構的能帶。這裡Ei是本徵半導體的費米能級,e 是費米能級Es和Ei的差。
理想MIS結構的定義如下:
 V=0時的平面能帶
V=0時的平面能帶(i)v=o時,半導體的能帶是平坦的(稱為平面能帶),換言之,v=o時,金屬和半導體的功函式相等。如右圖所示,這個條件可寫成下式:
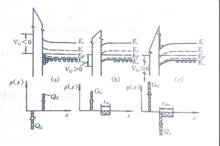 由p型半導體構成的理想MIS結構在各種VG下的表面勢和空間電荷分布
由p型半導體構成的理想MIS結構在各種VG下的表面勢和空間電荷分布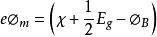 MIS結構
MIS結構 MIS結構
MIS結構(ii)v 時,對於p型半導體
(1)多數載流子堆積狀態
當金屬與半導體間加負電壓(指金屬接負)時,表面勢為負值,表面處能帶向上彎曲,。在熱平衡情況下,半導體內費米能級應保持定值,故隨著向表面接近,價帶頂將逐漸移近甚至高過費米能級,同時價帶中空穴濃度也將隨之增加。這樣,表面層內就出現空穴的堆積而帶正電荷。從圖中還可看到,越接近表面空穴濃度越高,這表明堆積的空穴分布在最靠近表面的薄層內。
(2)多數載流子耗盡狀態
當金屬與半導體間加正電壓(指金屬接正)時,表面勢Vs為正值,表面處能帶向下彎曲。這時越接近表面,費米能級離價帶頂越遠,價帶中空穴濃度隨之降低。在靠近表面的一定區域內,價帶頂位置比費米能級低得多,根據玻耳茲曼分布,表面處空穴濃度將較體內空穴濃度低得多,表面層的負電荷基本上等於電離受主雜質濃度。表面層的這種狀態稱做耗盡。
(3)少數載流子反型狀態
當加於金屬和半導體間的正電壓進一步增大時,表面處能帶相對於體內將進一步向下彎曲。這時,,表面處費米能級位置可能高于禁帶中央能量Ei,也就是說,費米能級離導帶底比離價帶頂更近一些。這意味著表面處電子濃度將超過空穴濃度,即形成與原來半導體襯底導電類型相反的一層,叫做反型層。反型層發生在近表面處,從反型層到半導體內部還夾著一層耗盡層。在這種情況下,半導體空間電荷層內的負電荷由兩部分組成,一部分是耗盡層中已電離的受主負電荷;另一部分是反型層中的電子,後者主要堆積在近表面區。
對於n型半導體,不難證明,當金屬與半導體間加正電壓時,表面層內形成多數載流子電子的堆積:當金屬與半導體間加不太高的負電壓時,半導體表面內形成耗盡層;當負電壓進一步增大時,表面層內形成有少數載流子空穴堆積的反型層。
表面空間電荷層的電場、電勢和電容
為了深入分析表面空間電荷層的性質,可以通過解泊松方程定量的求出表面層中電場強度和電勢分布,
取x軸垂直於表面指向半導體內部,並現定表面處為x軸原點。在表面空間電荷層中的電荷密度、場強和電勢都是x的函式,把表面近似看成是無限大面,以上各量將不隨y,z變,所以看成一維情況來處理。在這種情況下,空間電荷層電勢滿足的泊松方程為:
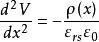 MIS結構
MIS結構 MIS結構
MIS結構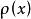 MIS結構
MIS結構式中 為半導體的相對介電常數, 為總的空間電荷密度,且由下式給出
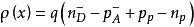 MIS結構
MIS結構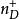 MIS結構
MIS結構 MIS結構
MIS結構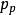 MIS結構
MIS結構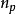 MIS結構
MIS結構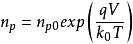 MIS結構
MIS結構其中 , 分別表示電離施主和電離受主濃度, 和 分別表示坐標x點的空穴濃度和電子濃度。若考慮表面層中經典統計 仍能使用的情況,則在電勢V的x點(取半導體內部電勢為零),電子和空穴濃度分別為
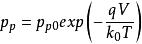 MIS結構
MIS結構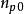 MIS結構
MIS結構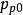 MIS結構
MIS結構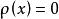 MIS結構
MIS結構和 分別表示半導體體內的平衡電子和空穴濃度。在半導體內部,假定表面空間電荷中電離雜質濃度為一常數,且與體內相等,則在半導體內部,電中性條件成立,故有 ,即
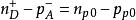 MIS結構
MIS結構將上述三式帶入泊松方程得
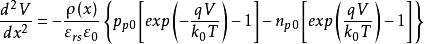 MIS結構
MIS結構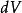 MIS結構
MIS結構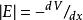 MIS結構
MIS結構將上式兩邊乘以 Bn並積分,並考慮 ,得
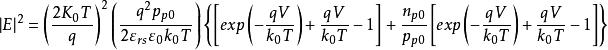 MIS結構
MIS結構令
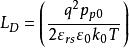 MIS結構
MIS結構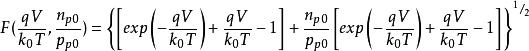 MIS結構
MIS結構則
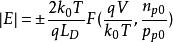 MIS結構
MIS結構 MIS結構
MIS結構當V大於零時取“+”號,小於零時取“-”號, 稱為德拜長度。F函式是表征半導體空間電荷層的一個重要參數。通過F函式,可以方便地表面空間電荷層的基本參數表達出來。
 MIS結構
MIS結構在表面處 ,可得到半導體表面處的電場強度為
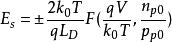 MIS結構
MIS結構 MIS結構
MIS結構根據高斯定理,表面的電荷密度 與表面處電場強度有以下關係:
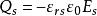 MIS結構
MIS結構 MIS結構
MIS結構將 代入上式,則
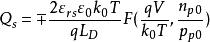 MIS結構
MIS結構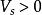 MIS結構
MIS結構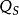 MIS結構
MIS結構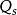 MIS結構
MIS結構當金屬電極為正,即 時, 用負號;反之, 用正號。從式中還能看到,表面層存在電場時,載流子濃度也發生變化。在單位面積的表面層中空穴的改變數(與體內比較)為
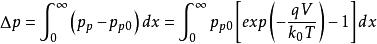 MIS結構
MIS結構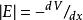 MIS結構
MIS結構 MIS結構
MIS結構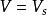 MIS結構
MIS結構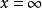 MIS結構
MIS結構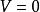 MIS結構
MIS結構考慮 ,並且 , 和 , ,則
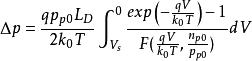 MIS結構
MIS結構同理可得
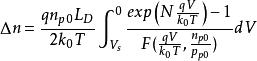 MIS結構
MIS結構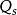 MIS結構
MIS結構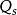 MIS結構
MIS結構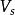 MIS結構
MIS結構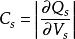 MIS結構
MIS結構以上兩式在計算電導時常要用到。根據 式子, 隨 而變,這相當於一電容效應。微分電容可由 求得為
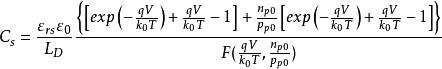 MIS結構
MIS結構上式給出的單位面積上的電容,單位為國際單位。於是套用上面得到的公式可定量的分析各種表面層的狀態
多數載流子堆積狀態
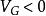 MIS結構
MIS結構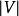 MIS結構
MIS結構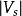 MIS結構
MIS結構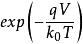 MIS結構
MIS結構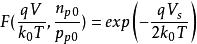 MIS結構
MIS結構仍以p型半導體來說明。當外加電壓 時,表面勢及表面層內部的電勢V都是負值,對於足夠大的 和 值。F函式只有含 的項其主要作用,其他項都可略去,得
將上面公式帶入之前公式,得
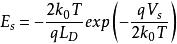 MIS結構
MIS結構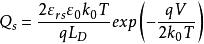 MIS結構
MIS結構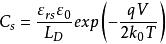 MIS結構
MIS結構上述三式分別表示出在多數載流子堆積狀態時,表面電場、表面電荷和空間電荷電容隨表面勢變化的關係
平帶狀態
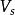 MIS結構
MIS結構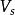 MIS結構
MIS結構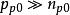 MIS結構
MIS結構外加電壓為零時,表面勢等於零,表面處能帶不發生彎曲,稱作平帶狀態。這時很容易求得F函式為零,從而Es=0,Qs=0。表面空間電荷層電容不能直接以Vs=0 得到,因為給出的時不穩定值。所以對原式 展開,近似取到二次方項,並令 趨近於零,並考慮到 ,最終得到
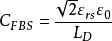 MIS結構
MIS結構耗盡狀態
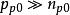 MIS結構
MIS結構當外加電壓為正但其大小還不足以使表面處禁帶中央能量彎曲到費米能級以下時,表面不會出現反型,空間電荷區處在空穴耗盡狀態,這時V和Vs都大於零,且 ,經過省略,則
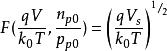 MIS結構
MIS結構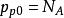 MIS結構
MIS結構又 帶入,得
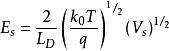 MIS結構
MIS結構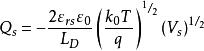 MIS結構
MIS結構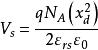 MIS結構
MIS結構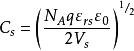 MIS結構
MIS結構也可以由“耗盡曾近似”直接處理,直接寫出電荷密度,泊松方程
反型狀態
隨著外加正電壓增大,表面出禁帶中央能值可以下降到費米能級以下,出現反型層。反型狀態分為強反型和弱反型兩種,以表面處少數載流子濃度是否超過體內多數載流子濃度為標誌來定。根據載流子濃度公式和玻爾茲曼統計可推得發生強反型的條件為:Vs≥2VB
在臨界強反型時
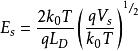 MIS結構
MIS結構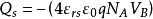 MIS結構
MIS結構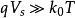 MIS結構
MIS結構當Vs 比2VB 大很多時,而且 時,有
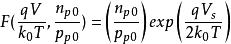 MIS結構
MIS結構將上式帶入原公式,得
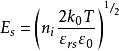 MIS結構
MIS結構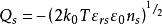 MIS結構
MIS結構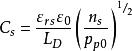 MIS結構
MIS結構MIS結構電容電壓特性
理想MIS結構的電容-電壓特性
考慮理想情況,由理論推導可得到
 MIS結構
MIS結構表明MIS結構電容相當於絕緣層電容和半導體空間電荷層電容串聯,下面討論理想MIS結構的電容電壓特性。
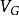 MIS結構
MIS結構當偏壓 為負值時半導體表面處於堆積狀態,將此時的空間
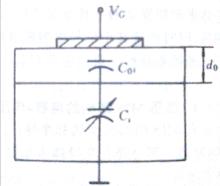 MIS結構的等效電路
MIS結構的等效電路電荷層的電容公式帶入上式中,得到
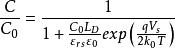 MIS結構
MIS結構可以看出當加較大的負偏壓時C=C0,此時的MIS的電容不隨外加電壓的變化。當|VG|較小時,|Vs|也很小,上式分母第二項變大,此時C/C0隨|Vs| 的減小而減小,如圖中BC段所示。
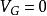 MIS結構
MIS結構當 時,同理將之前所求電容公式代入,得
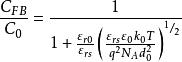 MIS結構
MIS結構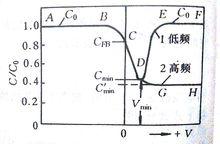 MIS結構的電容電壓曲線
MIS結構的電容電壓曲線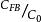 MIS結構
MIS結構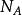 MIS結構
MIS結構在利用C-V特性測量表面參數時常需計算 的值因此根據上式做了一簇曲線以供查閱。在圖中可以看到若絕緣層厚度一定,NA越大CFB/C0 也越大,這是因為表面空間電荷層隨 增大而變薄所致。另一方面絕緣層厚度越大,C0越小,CFB/C0 也越大。
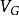 MIS結構
MIS結構當金屬與半導體間外加偏壓 為正但不足以使半導體表面反型時,空間電荷區處於耗盡狀態,同理將此時的電容公式帶入,得
 MIS結構
MIS結構上式表明,MIS結構電容隨表面勢變化情況。因VG=V0+VS, V0=-Qs/c0,,又由之前得到的Qs公式,求解Vs,化簡整理後得
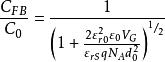 MIS結構
MIS結構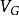 MIS結構
MIS結構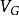 MIS結構
MIS結構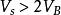 MIS結構
MIS結構上式表示在耗盡狀態時C/C0 隨 變化情況。從上式可以看出,當 增加時,C/C0 將減小。如圖中CD段表示當外加電壓增大到 時,此時耗盡層寬度保持在極大值,表面處出現反型層,同理得到
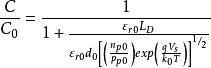 MIS結構
MIS結構上式表示在強反型情況下時C/C0 隨表面勢的變化情況。可以看出上式分母中第二項趨近於零,這時C=C0 ,即MIS的電容又上升到等於絕緣層的電容,如圖中EF段表示。
當信號變為高頻時上式不再適用,圖像如GH段所示
金屬與半導體功函式差對C-V特性的影響
為了具體起見,以鋁-二氧化矽-矽組成的MOS結構為例來說明,並設半導體矽為P型的。將鋁和p型矽連線起來,由於p型矽的功函式一般較鋁為大,電子將從金屬流向半導體中。因此在p型矽表面層內形成帶負電的空間電荷層,而在金屬表面產生正電荷。這些正負電荷在二氧化矽及矽表面層內產生指向半導體內部的電場,並使矽表面層內能帶發生向下彎曲。同時矽內部的費米能級相對於金屬的費米能級就要向上提高,到兩者相等達到平衡,所以半導體中電子的電勢能相對於金屬提高的數值為
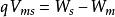 MIS結構
MIS結構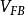 MIS結構
MIS結構由於二者功函式不同,即使外加偏壓為零,但半導體表面層並不處於平帶狀態,所以為了恢復這一狀態,必須在鋁和半導體矽之間加一個負電壓,這個負電壓就是 。顯然:
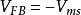 MIS結構
MIS結構絕緣層中電荷對C-V特性的影響
一般在MIS結構的絕緣層內總是或多或少地存在著電荷的,設絕緣層中有一薄層電荷,其單位面積上的電量為
Q,離金屬表面的距離為x在無外加電壓時,這薄層電荷將分別在金屬表面和半導體表面層中感應出相反符號的電荷。由於這些電荷的存在,在半導體空間電荷層內將有電場產生,能帶發生彎曲。這就是說,雖然未加外電
壓,但由於絕緣層內電荷的作用,也可使半導體表面層離開平帶狀態。為了恢復平帶狀態,同前一樣,必須在金屬板上加一定的偏壓。例如,Q是正電荷時,在金展與半導體表面層中將感應出負電荷空間電荷層發生能帶向下彎曲。若在金屬板上加一逐漸增大的負電壓,金屬板上的負電荷將隨之增加,由Q發出的電力線特更多地終止於金屬表面。半導體表面層內的負電荷就會不斷減小,如果外加負電壓增大到這樣程度,以致使半身體表面層內的負電荷完全消失了。這時,在半導體表面層內。由薄層電荷所產生的電場完全被金屬表面負電荷產生的電場所抵消,表面層能帶的彎曲也就完全用失。
這時,經計算
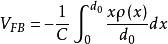 MIS結構
MIS結構當上述二者都存在時
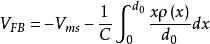 MIS結構
MIS結構
