LRL矢量

在經典力學裡，拉普拉斯-龍格-楞次矢量（簡寫為 LRL 矢量）主要是用來描述，當一個物體環繞著另外一個物體運動時，軌道的形狀與取向。典型的例子是行星的環繞著太陽公轉。在一個物理系統里，假若兩個物體以萬有引力相互作用，則 LRL 矢量必定是一個運動常數，不管在軌道的任何位置，計算出來的 LRL 矢量都一樣；也就是說， LRL 矢量是一個保守量。更廣義地，在克卜勒問題里，由於兩個物體以有心力相互作用，而有心力遵守反平方定律，所以，LRL 矢量是一個保守量。
氫原子是由兩個帶電粒子構成的。這兩個帶電粒子以遵守庫侖定律的靜電力互相作用．靜電力是一個標準的反平方有心力。所以，氫原子內部的微觀運動是一個克卜勒問題。在量子力學的發展初期，薛丁格還在思索他的薛丁格方程的時候，沃爾夫岡·泡利使用 LRL 矢量，關鍵性地導引出氫原子的發射光譜。這結果給予物理學家很大的信心，量子力學理論是正確的。
在經典力學與量子力學裡，因為物理系統的某一種對稱性，會產生一個或多個對應的保守值。 LRL 矢量也不例外。可是，它相對應的對稱性很特別；在數學裡，克卜勒問題等價於 一個粒子自由地移動於 四維空間的三維球；所以，整個問題涉及四維空間的某種旋轉對稱。

拉普拉斯-龍格-楞次矢量是因皮埃爾-西蒙·拉普拉斯，卡爾·龍格，與威爾漢·楞次而命名。它又稱為拉普拉斯矢量，龍格-楞次矢量，或楞次矢量。有趣的是，LRL 矢量並不是這三位先生髮現的！這矢量曾經被重複地發現過好幾。它等價於天體力學中無量綱的離心率矢量。發展至今，在物理學裡，有許多各種各樣的 LRL 矢量的推廣定義；牽涉到狹義相對論，或電磁場，甚至於不同類型的有心力。概論

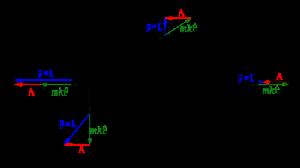
在一個物理系統里，在任意保守的有心力的作用下（參閱保守力），一個粒子的運動，都會擁有至少四個運動常數；能量與角動量 的三個分量皆為運動常數。粒子的軌道被限制於一個平面。粒子的動量 和從力中心點的位置到粒子位置的位移 粒子的運動平面垂直於角動量 。用方程表示，L*R=0 。
LRL 矢量 ，也肯定地包含於粒子的運動平面。可是，只有當有心力遵守反平方定律時， 才是常數矢量。對於別種有心力， 不是常數矢量，其大小與方向都會改變。假若有心力近似地遵守反平方定律，則 的大小近似常數，而方向會緩慢地轉動。對於所有的有心力，我們可以定義一個廣義 LRL 矢量，但是，這廣義矢量通常並沒有解析解，假若有，也會是一個非常複雜的函式。

歷史

在重要的克卜勒問題中， LRL 矢量 是一個運動常數，時常用來描述天文軌道，例如行星的運動。然而，物理學家對它並不熟悉，這很可能是因為與動量與角動量相比，它比較難以被直覺地理解內涵的物理。因此，在過去三個世紀裡，它曾被重複地發現過許多次。1710 年，在一個不著名的義大利學刊里，雅各布·赫爾曼最先發表了關於 LRL 矢量的論文。在導引一個軌道方程的過程中，他計算出 LRL 矢量的大小， 是保守的；並且導引出此案例與橢圓軌道離心率的關係。稍後，赫爾曼把這結果告訴約翰·伯努利，他的恩師。伯努利又更進一步地導引出 LRL 矢量的方向。這樣，LRL 矢量得到了它的現代形式。所以，不容質疑地，LRL 矢量是赫爾曼和伯努利共同發現的。
在那個世紀末尾，皮埃爾-西蒙·拉普拉斯又重新地發現了 LRL 矢量的保守性；稍微不同地，他的導引使用的是分析方法，而不是幾何方法。十九世紀中葉，威廉·盧雲·哈密頓導引出全等的離心率矢量。他用離心率矢量來證明，在反平方有心力作用下，速端曲線顯示出，粒子動量矢量的頭部呈圓形移動。二十世紀初，約西亞·威拉德·吉布斯，套用矢量分析，導引出同樣的矢量。後來，卡爾·龍格將吉布斯的導引，納入自己所寫的一本廣受歡迎的，關於矢量的，德文教科書內，成為其中的一個例題。1924 年，威爾漢·楞次發表了一篇關於氫原子的舊量子論的論文。在這篇論文中，他引用龍格所寫的教科書的例題為參考。1926 年， 沃爾夫岡·泡利用 LRL 矢量與矩陣力學，而不是薛丁格方程，來導引氫原子的光譜。這傑作說服了大多數物理學家，使他們覺得量子力學理論是正確的。