定義
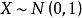 F分布
F分布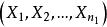 F分布
F分布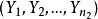 F分布
F分布若總體 , 與 為來自X的兩個獨立樣本,設統計量
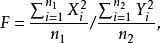 F分布
F分布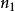 F分布
F分布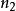 F分布
F分布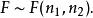 F分布
F分布則稱統計量F服從自由度 和 的F分布,記為
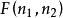 F分布
F分布分布的機率密度為
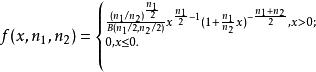 F分布
F分布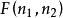 F分布
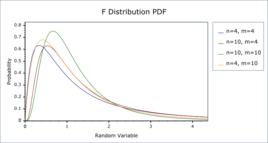
F分布分布的機率密度函式圖像如圖1所示
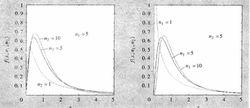 圖1
圖1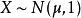 F分布
F分布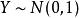 F分布
F分布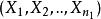 F分布
F分布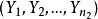 F分布
F分布若總體與總體獨立,為來自X的一個樣本,為來自Y的一個樣本,則統計量
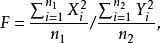 F分布
F分布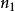 F分布
F分布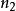 F分布
F分布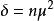 F分布
F分布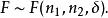 F分布
F分布則稱統計量F服從自由度為和,非中心參數為的非中心F分布,記為
性質
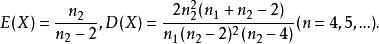 F分布
F分布性質1:
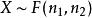 F分布
F分布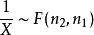 F分布
F分布性質2: 設,則。
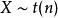 F分布
F分布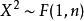 F分布
F分布性質3:設,則。
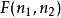 F分布
F分布性質4:分布的分布函式可用標準常態分配的分布函式來逼近。即
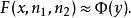 F分布
F分布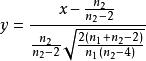 F分布
F分布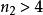 F分布
F分布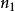 F分布
F分布其中,(,充分大)。
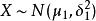 F分布
F分布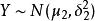 F分布
F分布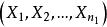 F分布
F分布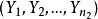 F分布
F分布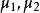 F分布
F分布性質5: 若總體與獨立,為來自X的一個樣本,為來自Y的一個樣本,為已知參數。則統計量
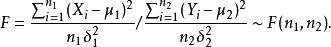 F分布
F分布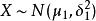 F分布
F分布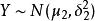 F分布
F分布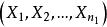 F分布
F分布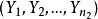 F分布
F分布性質6: 若總體與獨立,為來自X的一個樣本,為來自Y的一個樣本,則統計量
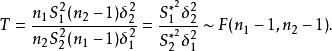 F分布
F分布