簡介
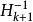 DFP法
DFP法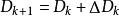 DFP法
DFP法DFP算法是以William C Davidon、 Roger Fletcher 、 Michael J. D. Powell 三個人的名字的首字母命名 的,它由Davidon於1959年首先提出,後經Fletcher和Powell加以發展和完善,是最早的擬牛頓法、該算法的核心是:通過 疊代的方法,對 做近似,疊代格式為 ,k=1,2,……(2.22)
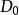 DFP法
DFP法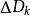 DFP法
DFP法其中的 ,通常取為單位矩陣I。因此,關鍵是每一步的校正矩陣 如何構造。
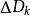 DFP法
DFP法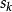 DFP法
DFP法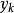 DFP法
DFP法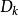 DFP法
DFP法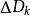 DFP法
DFP法注意,疊代格式(2.22)將嵌套在牛頓法中,因此,我們猜想 可能與 , ,和 發生關聯。這裡,我們採用“待定法”,即首先將 協待定成某種形式,然後結合擬牛頓條件來進行推導。
對於擬牛頓方程:
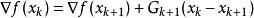 DFP法
DFP法化簡可得:
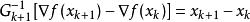 DFP法
DFP法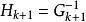 DFP法
DFP法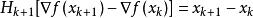 DFP法
DFP法令 ,可以得到:
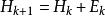 DFP法
DFP法在DFP校正方法中,假設:
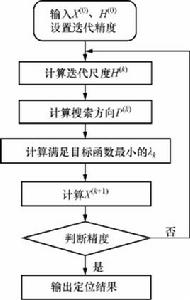
算法流程
 DFP法
DFP法DFP擬牛頓法的算法流程如下:
效能特點
DFP變尺度法綜合了梯度法、牛頓法的優點而又避棄它們各自的缺點,只需計算一階偏導數,無需計算二階偏導數及其逆矩陣,對目標函式的初始點選擇均無嚴格要求,收斂速度快,這些良好的性能已作闡述。對於高維(維數大於50)問題被認為是無約束極值問題最好的最佳化方法之一。1.DFP 公式恆有確切解2.LIFP 法搜尋方向的共扼性3.DFP 算法的穩定性。
為提高實際計算的穩定性,除提高一維搜尋的精度外,通常還將進行n次(n 為目標函 數的維數)疊代作為一個循環, 將變尺度矩陣重置為單位矩陣I,並以上一循環的終點作為起 點繼續進行循環疊代,這己反映在疊代過程和算法框圖之中。