簡介
A–B 效應,全名 阿哈羅諾夫-玻姆效應,是個物理學實驗。它證明即使在磁場為零的區域,仍舊會存在磁效應,然而,這並不能用來測量磁矢勢,因為只有磁通量會出現在表達效應的公式里,而且整個理論始終維持規範不變性。阿哈羅諾夫-玻姆效應是量子力學和電動力學發展史上的重要實驗,說明了量子力學的非局域性質。
“A–B”這個名稱取自在1959年設計這個實驗的兩位理論物理家亞基爾·阿哈羅諾夫(YakirAharonov)和戴維·博姆(DavidBohm)姓名的首字,前者因這個實驗而得到1998年沃爾夫物理學獎。巧合的是,物理學家也用A表示磁矢勢,B表示磁場,賦予A–B 效應這個名字更加深刻的涵義。
研究
起源
1959年,阿哈羅諾夫(Y.Aharonov)和玻姆(D.Bohm)發表一篇論文,該論文認為,在電子運動的空間中,無論是否存在電磁場,電子波函式的位相都會受到空間中電磁勢的影響。由此他們做出結論,在量子理論中,電磁勢要比經典電磁理論中的電場與磁場強度更有意義。他們同時建議了幾種能證實上述理論的實驗途徑。
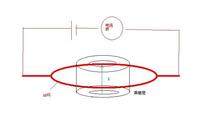
入射電子束在A點被分為兩束,磁場B處於與圖面垂直的螺線管中。兩支電子束在觀察屏S處相遇形成干涉。在電子經過的路徑上,磁感應強度為零,但是磁矢勢A卻不為零。正是由於磁矢勢的存在,使兩束電子產生了附加位相差,該值恰好為電子路徑包圍磁通量的e/h倍。他們認為,改變B值,影響磁通量,將使位相差改變,電子的干涉圖樣就會受到影響。同樣,如果在兩束電子的路徑上各加一隻金屬筒,當電子進入筒時,在兩筒上加不同的電勢,電子出離筒後,即將電勢撤消,電子束也會因電勢的不同產生附加位相差,導致干涉圖樣變化。發表這一理論的時候,阿哈羅諾夫正在美國南卡羅萊納大學物理與天文學系及以色列特拉維夫大學物理系任教。阿哈羅諾夫很善於研究那些通常被人們忽視的物理現象。他所預言的一些效應先後被實驗證實,由於具有重要意義,都在物理界引起不小的波瀾。AB效應就是其中一個,是他與任教於倫敦大學的玻姆共同提出的。
實驗證實
1960年,AB效應被錢伯斯(Chambers)實驗證實。隨後,美國、聯邦德國、義大利等幾個實驗小組也陸續進行了類似的實驗,都支持了這一預言。儘管如此,由於電子的波長很短,限制磁場的區域很小,螺線管半徑不但必須很小,長度還要無限長,這些條件很難得到實驗保證,因而有人對實驗結果的可靠性表示懷疑。直到80年代中期,日本物理學家用超導材料將磁場禁止以後,所證實的AB效應才被物理界普遍接受。AB效應的證實對物理學的影響是深遠的。本世紀初,相對論與量子論的問世,給人類對物理世界的認識帶來了嶄新的圖象與觀念,使物理學發生了天翻地覆的變化。然而,麥克斯韋電磁理論卻仍然保持原有風貌,似乎不受其影響。這一點卻也不難理解,因為麥克斯韋方程自身的協變性,使其天然地與相對論的要求和諧一致。此外,這一方程又能滿足電磁波量子性的要求。然而,深究起來,在經典電磁理論與量子理論之間,也有一點不一致,這就是所謂的AB之爭。
兩個基本量
從表面看來,AB之爭所涉及的似乎只是兩個物理量的問題。在經典電磁理論中,描述場的兩個基本量是電場強度和磁感應強度,電標勢是在電場基礎上,利用環路積分引入的,它具有物理意義,雖然數值不唯一,卻是可以實驗測量的。磁矢勢卻不同,雖然它也是在磁場的基礎上引入的,卻不具有明確的物理意義,數值不唯一,也不能實驗觀測。因此,在經典電磁理論中,常把作為描述磁場的基本量,純屬於為計算方便而引入的過渡量或輔助量。
本質
在量子電動力學中,A和B的地位則皆然相反。出現在方程中的電磁量是Φ和A,而不再是E與B。A與B相比,A成為第一位的物理量。A與B哪一個更為本質的問題,在本世紀20年代量子理論創建時即被提出,直到1959年才被阿哈羅諾夫及玻姆所解決。
AB效應表明,描述磁場的矢量與磁場相比,是更為本質的。這一點僅能通過量子效應才能顯現出來。對固體材料AB效應的觀察是近幾年來的事。最初觀察的是線度很小的金環。金環的直徑0.8μm,寬0.4μm,附在矽片上。沿直徑接入電極後,通過電流測量金環的電壓。整個實驗在0.06K的超低溫下進行。垂直環面加入磁場,電子沿金環的各一半,分兩路流出。在匯合處,兩路電子波產生干涉,由合振幅的模即可確定磁阻。實驗結果發現,金環磁阻隨磁場周期性地變化。振盪周期與樣品面積的乘積,恰好與AB效應所要求的h/e值相等,從而證實了固體材料中,電子波的量子干涉AB效應。AB效應的觀測,很自然地涉及到納米物理學的進展。觀測到該效應的前提條件是電子波能現出可觀測到的相干性。在真空條件下,電子束的干涉比較容易觀察到,然而在固體材料中,電離雜質與晶格的振動都能破壞材料的理想周期性,因而造成電子散射。由於電離雜質的質量比電子大得多,對電子靜電作用的結果,離子受影響較小,電子卻偏離了原來方向的運動而發生散射。這種散射屬於彈性散射,它雖然能使電子波的位相發生變化,卻不改變電子波的相干性;然而,晶格振動造成的散射,涉及聲子的發射與吸收,屬於非彈性散射,將嚴重地影響電子波的相干性。可見,若能在固體材料中觀察到AB效應,對材料的純度要求並不高,但對材料的線度有一定的要求。因為電子必須在受到非彈性散射之前,也即在連續兩次非彈性散射發生之間,穿過樣品。根據電子的平均自由程時間,可以計算出電子波相干長度λ。一般金屬在溫度1K下,相干長度可達μm數量級。在現代科技條件下,製造長度在μm以內、線寬在幾十個nm以內的環狀樣品已不困難,因而這一領域的研究得以迅速發展。當材料的線度L≤λ時,材料內將可能包含10^8~10^11個原子,因此,無論觀測的對象、觀測的手段以及觀測的量值(如電流或電壓等)都仍屬於巨觀範疇。然而實驗的結果卻能反映電子的波動性和體系微觀物理的規律,這再一次表明,納米結構物理學研究的特殊意義。它開闢了用巨觀領域的研究方法與概念探討微觀物理規律的新途徑。
繼續發展
AB效應的研究仍在繼續發展中。由於電磁場是一種最簡單的U(1)規範場,人們很自然地會聯想到,是否能把AB效應推廣到其它規範場中。華裔美籍物理學家楊振寧和吳大峻曾在一篇論文中討論過楊—米爾斯SU(2)規範場的AB效應問題。而阿哈羅諾夫和卡謝又於1984年根據電與磁的對偶性,提出了AC效應的預言。
提出與證實
AC效應的提出與證實,是納米物理學的又一重要進展。它由阿哈羅諾夫與在特拉維夫大學的同事卡謝(A.Casher)共同提出來的,用他們兩人姓氏的第一個字母,簡稱為AC效應。阿哈羅諾夫與卡謝認為,如果存在有磁場作用的AB效應,根據電與磁的對偶性,一定會存在著一種AB效應的對偶效應。在電磁場的張量相對論理論中,電磁場張量Fuv應有16個分量。由於這一張量的反對稱性,四個對角元素為零外,兩側對稱量等量反號,所余的獨立分量即只有6個,這就是3個電場分量與3個磁場分量。根據張量理論,電場與磁場互為對偶場,當電與磁量按一定規則互換時,對應的物理規律相互對偶。這樣,在相應的AB效應示意圖中,把螺線管替換成一條垂直圖面的無限長帶正電線,把電子束替換成中子束。中子不帶電,卻由於其自旋而具有磁矩,令中子束中,每箇中子的磁矩與帶電線平行。AB效應中,電子不受磁場力;AC效應中,中子不受電場力。AB效應中,由於磁矢勢的存在,引起電子相移;AC效應中,將由於電勢Φ的存在,引起中子相移發生。阿哈羅諾夫與卡謝還預言,中子相移的大小,與荷電線的帶電密度成正比,對於一般的荷電線密度,他們估算結果,相移約為1.5mrd。1989年,他們的這一預言被墨爾本大學、密蘇里大學和紐約州立大學組成的聯合研究組所實驗證實。實驗中使用的帶電線為45kV的細絲高壓正電極,而中子束來源於反應堆。由於很難獲得磁偶極矩順向排列的極化中子束,他們把非極化的中子束加了補償措施,以消除非極化的影響。先使中子束通過一個狹縫,經過單晶矽片分為兩束通過帶電線的兩側附近,再經第二片單晶矽片折射,改變方向後相交。分別用兩台3He正比計數器測量。為使中子數累計到理論所要求的10 個,整個實驗持續了幾個月。最後測得相移為2.19±0.52mrd,這個結果證實了AC效應的存在。
磁場阿哈羅諾夫-玻姆效應
量子力學理論內,對在磁場裡運動做以下處理:動量算符加入矢勢項
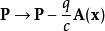 AB效應
AB效應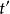 AB效應
AB效應和粒子波函式在從時間 t到期間兩點間運動的波幅多得到一個複數相:
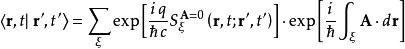 AB效應
AB效應 AB效應
AB效應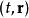 AB效應
AB效應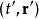 AB效應
AB效應其中是任意從到的路徑。
因此粒子如果透過某連線兩點的路徑1從一點運動到另外一點,相比磁場強度為零的差別是多出的波函式復相:
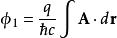 AB效應
AB效應。
如果有另外連線同樣兩點的路徑2,那波函式將得到不同的復相。兩路徑得到相位之差為:
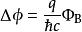 AB效應
AB效應 AB效應
AB效應其中為兩路徑圍起面積的磁通量。
雖然波函式的相位在量子理論里不是可測量物理量,但是相位差可以透過干涉實驗來測量。因此此矢勢引起的相位差可以透過在電子雙縫實驗的雙縫後加入磁場觀察。如圖示。雖然電子的路徑經過的地方磁場強度為零,但是有大於零的矢勢強度。因此電子在螢幕上的干涉圖樣得到比沒有磁場的時候平移。實際的實驗由日立公司的科學家率先完成。