階乘
 階乘
階乘 階乘,也是 數學里的一種 術語。
階乘指從1乘以2乘以3乘以4一直乘到所要求的數。
計算方法
正整數階乘指從1乘以2乘以3乘以4一直乘到所要求的數。例如所要求的數是4,則階乘式是1×2×3×4,得到的 積是24,24就是4的階乘。 例如所要求的數是6,則階乘式是1×2×3×……×6,得到的積是720,720就是6的階乘。例如所要求的數是n,則階乘式是1×2×3×……×n,設得到的積是x,x就是n的階乘。
表示方法
任何大於1的 自然數n階乘表示方法:n!=1×2×3×……×n
或
n!=n×(n-1)!
20以內數的階乘
以下列出0至20的階乘:0!=1,注意(0的階乘是 存在的)
1!=1,
2!=2,
3!=6,
4!=24,
5!=120,
6!=720,
7!=5,040,
8!=40,320
9!=362,880
10!=3,628,800
11!=39,916,800
12!=479,001,600
13!=6,227,020,800
14!=87,178,291,200
15!=1,307,674,368,000
16!=20,922,789,888,000
17!=355,687,428,096,000
18!=6,402,373,705,728,000
19!=121,645,100,408,832,000
20!=2,432,902,008,176,640,000
另外,數學家定義,0!=1,所以0!=1!
而當n≥5時,n!的個位數字都是0.
舉例
所要求的數是4,則階乘式是1×2×3×4,得到的積是24,24就是4的階乘。 例如所要求的數是6,則階乘式是1×2×3×……×6,得到的積是720,720就是6的階乘。例如所要求的數是n,則階乘式是1×2×3×……×n,設得到的積是x,x就是n的 階乘。在表達階乘時,就使用“!”來表示。如h階乘,就表示為h!
階乘一般很難計算,因為積都很大。
以下列出1至10的階乘。
1!=1,
2!=2,
3!=6,
4!=24,
5!=120,
6!=720,
7!=5040,
8!=40320
9!=362880
10!=3628800
另外,數學家定義,0!=1,所以0!=1!
通常我們所說的階乘是定義在自然數範圍里的,小數沒有階乘,像0.5!,0.65!,0.777!都是錯誤的。
但是,有時候我們會將Gamma函式定義為非整數的階乘,因為當x是正整數n的時候,Gamma函式的值是n-1的階乘。
伽瑪函式(Gamma Function)
Γ(x)=∫e^(-t)*t^(x-1)dt (積分下限是零上限是+∞)(x0,-1,-2,-3,……)
運用積分的知識,我們可以證明Γ(x)=(x-1) * Γ(x-1)
所以,當x是整數n時,Γ(n) = (n-1)(n-2)……=(n-1)!
這樣Gamma 函式實際上就把階乘的延拓。
雙階乘
雙階乘用“m!!”表示。
當m是自然數時,表示不超過m且與m有相同奇偶性的所有正整數的乘積。如:
(2n-1)!!=1×3×5×···×(2n-1)
2n!!=2×4×8×···×2n
當m是負奇數時,表示絕對值小於它的絕對值的所有負奇數的絕對值積的倒數。
當m是負偶數時,m!!不存在.
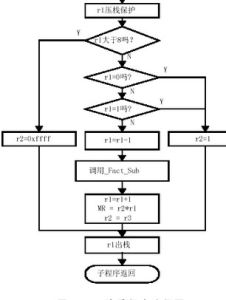
計算機階乘
Python語言中
在Python中, 可以很方便的用更為簡潔方式實現階乘的計算:
deffactorial(n)
ifn==1
return1
else
returnfactorial(n-1)*n
C語言中
在C語言中,使用循環語句可以很方便的求出階乘的值,下面介紹一個很簡單的階乘例子。(因為網上多數是比較麻煩的方法)
¤【計算出“ 1!+ 2!+ 3!+ …… + 10!”的值是多少?】
#include
int main(void)
{
long x, j=1, sum=0;
for ( x=1; x 0 )
e = n * f(n - 1);
cout if($n1){