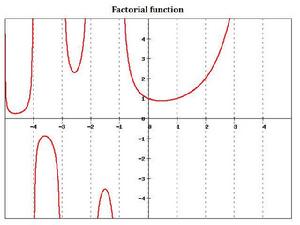
定義
一個正整數的 階乘（英語： factorial）是所有小於及等於該數的正整數的積，並且有0的階乘為1。自然數n的階乘寫作n!。1808年，基斯頓·卡曼引進這個表示法。
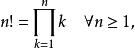階乘函式亦即n!=1×2×3×...×n。階乘亦可以遞歸方式定義：0!=1，n!=(n-1)!×n。
階乘亦可定義於整個實數（負整數除外），其與伽瑪函式的關係為：
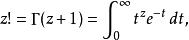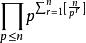階乘函式
階乘函式n!可質因子分解為 ，如6!=2×3×5。
計算
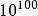階乘函式計算n!時，當n不太大時，普通的科學計算機都可以計算，能夠處理不超過 數值的計算機可以計算至69!。
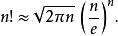階乘函式當n很大時，可以用斯特林公式估計：
更精確的估計是：
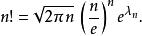階乘函式
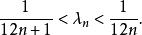階乘函式其中
變化
定義擴展
階乘的定義可推廣到複數，其與伽瑪函式的關係為：
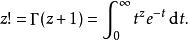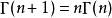階乘函式
階乘函式伽瑪函式滿足 。
遞進/遞降階乘
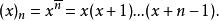階乘函式遞進階乘：
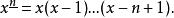階乘函式遞降階乘：
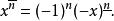階乘函式雙階
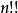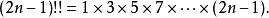階乘函式
階乘函式表示雙階乘，其定義為：
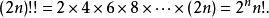階乘函式廣義的雙階乘
無視上述定義的n!!因為即使值的N，雙階乘為奇數可擴展到最實數和複數z的注意到，當z是一個正的奇數則：
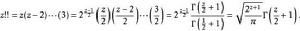階乘函式z!!定義為所有複數除負偶數。
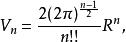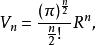階乘函式
階乘函式使用它的定義，半徑為R的n維超球其體積可表示為： n=1,3,5,... n=2,4,6,...
多重階乘
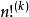階乘函式被稱為n的k重階乘，定義為：
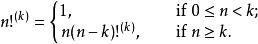階乘函式廣義的多重階乘
能將 多重階乘推廣到複數（甚至是四元數）：
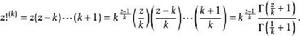階乘函式hyper階乘
hyper階乘（hyperfactorial有時譯作 過度階乘）寫作H（n），其定義為：
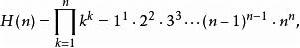階乘函式hyper階乘和階乘差不多，但產生更大的數。hyper階乘的增長速度卻並非跟一般階乘在大小上相差很遠。 前幾項的hyper階乘為：
1,4,108, 27648, 86400000, ...
超級階乘
1995年，尼爾·斯洛恩和西蒙·普勞夫定義了超級階乘（superfactorial）為首n個階乘的積。一般來說
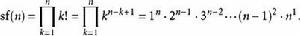階乘函式自然數階冪
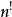階乘函式階冪也稱 疊冪或者 重冪記作 （感嘆號!寫在自然數的右上角），它的定義是將自然數1至n的數由大到小作冪指數重疊排列，數學定義如下：
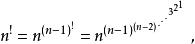階乘函式其中n ≥ 1，前幾項的重冪數為：
1 , 2 , 9 , 262144 , ...
第5個重冪數是一個有183231位阿拉伯數字組成的超大自然數。
二次階冪：
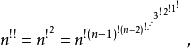階乘函式相應地，m次階冪定義如下：
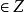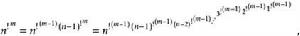階乘函式
階乘函式其中n，m≥1，且n，m。
