簡介
研究歷史
橢圓偏振光的特徵由方位(長軸方位) 形狀(短長軸之比彌偏心率)和旋向確定,稱偏振態。研究橢圓偏振光的教學方法共有四種:即三角函式法、瓊斯(R ·C - Jones)矢量矩陣法、斯托克斯 - G ·Stokes)參量法和龐加萊(H - Poincare)球法。
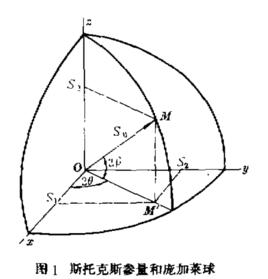
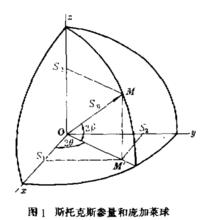 斯托克斯參量和龐加萊球
斯托克斯參量和龐加萊球龐加菜球是研究任一偏振態的圖示方法。對於龐加萊球的導出,從查閱的國內外文獻資料來看,都是根據龐加萊於1892年提出的理論,即從斯托克斯參量入手引進球體的。
特徵
球的兩極表征的是左、右旋圓偏振光:赤道上各點表{iE的是振動方向不同的線偏振光:上半球表征的是左旋橢圓偏振光:下半球表征的是右旋橢圓偏振光等等。
龐加萊球模型
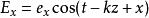 龐加萊球
龐加萊球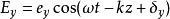 龐加萊球
龐加萊球設沿OZ 方向傳播的橢圓偏振光的兩個線性偏振分量為 , 兩個線性偏振分量的相位差δ=δ-δ令tgα=e/e則橢圓的方位角Ψ滿足
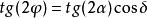 龐加萊球
龐加萊球橢圓率角Χ滿足
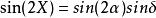 龐加萊球
龐加萊球其中方位角Ψ是橢圓主軸與X 軸正方向之間的夾角,它決定了橢圓在該平面內的取向(-π/2 <Ψ<π/2)。橢圓率角X定義為tgX = ±b /a,其中a 為橢圓半長軸,b為橢圓半短軸 X 的正負分別對應於右旋偏振和左旋偏振。 對於TE平面波的各種可能偏振態,可以用斯托克斯參數進行表示。斯托克斯參數的定義為
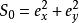 龐加萊球
龐加萊球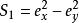 龐加萊球
龐加萊球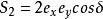 龐加萊球
龐加萊球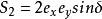 龐加萊球
龐加萊球顯然S =S + S + S 所以式中只有3 個變數是獨立的 且有
tg(2Ψ)=S/S
sin(2X)=S/S
理想情況下(即在無損傳輸時)有S = 常數 所以SS S所表示的是一個球面。S =1 的球就是龐加萊球。 球殼上各點與光的全偏振態一一對應。
龐加萊球表象
龐加萊球的角量(Ψ、x) 具有特定的意義,是描述單色光波偏振態的兩個重要參量。
龐加萊球的赤道
龐加萊球的赤道是直線偏振光的集合,振動平面隨著經度的增大而旋轉。
赤道上S = 0 , 有φ= nπ(n 為零或整數) ,或a =0 或a = 0;設OX與OS軸平行,OS軸與球面的交點M 處,S=S ,而S = S = 0 ,於是有a = 0 ,即點M 表征著振動方向平行OX軸的直線偏振狀態;在OS2 軸與球面的交點N 處,S3 = 0、S = 0、S = S ,於是有a = a ,Ψ = 45°,即點N 表征與OX軸成45°角的直線偏振狀態;同理M的對稱點M′表征著與OX軸成90°角即平行OY方向的直線偏振態1。對經度為2Ψ 的赤道上一點Q 有
S=a +a
S= a a = Scos2Ψ = Scos Ψ -Ssin Ψ
S = 2 aa = Ssin2Ψ = 2 ScosΨsinΨ
得a = ScosΨ ,a = SsinΨ。由此可知,該點Q 表征著與OX軸成Ψ 角的直線偏振。
龐加萊球的南、北極點
龐加萊球的南、北極點所表征的偏振態如下。
對於該兩極點,S= S = 0、S = S3 ,從而有ax = ay ,φ= nπ+π/ 2,北極點S > 0 ,φ= 2nπ+π/ 2 ,即X方向的振動超前於Y方向π/ 2 ,於是該北極點表征右旋圓偏振光。同理可知,南極點表征左旋圓偏振光。
龐加萊球上的其它任一點
龐加萊球上的其它任一點P ( S1 、S2 、S3) 表征著橢圓偏振態。
角Ψ 表示橢圓的取向,它是橢圓長軸與OX的夾角(0 ≤Ψ ≤ π) 同一經線上各點表征著長軸具有相同取向的不同橢圓偏振態。角X用來表示橢圓的形狀,也就是長短半軸(a ,b) 之比,tgx = ±b/ a ,可見龐加萊球的緯線代表等橢圓率線1 當0 < x ≤π/4 時,S3 > 0 即φ> 0 ,為右旋橢圓偏振光;當-π/4 ≤x < 0 時S3< 0 即φ< 0 ,為左旋橢圓偏振光。