簡介
無窮遠奇點是平面奇點的一種推廣,用於研究平面系統的軌線在平面上無窮遠處的性態。
龐加萊球面
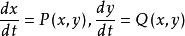 無窮遠奇點
無窮遠奇點龐加萊(Poincare,(J.-)H.)把(x,y)平面上的系統 的軌線投影到與(x,y)平面相切於原點的一個單位球面S上,後人就稱此球面S為龐加萊球面。
如下圖取坐標系。
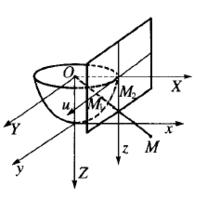 圖1
圖1在(X,Y,Z)空間中,(x,y)平面上的點M可表示為(x,y,1)。取球心投影,即連結M與球心(0,0,0),其連線與球面S交於兩點,取定下半球面的一點M(X,Y,Z)。這樣就把(x,y)平面上的點一一對應到龐加萊下半球面上,(x,y)平面上的無窮遠即對應於S的赤道:X +Y =1,Z=0。
為便於寫出微分方程研究Z=0上各點鄰近的性態,再把下半球面上的點投影到一個適當的鉛直平面上。
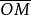 無窮遠奇點
無窮遠奇點 無窮遠奇點
無窮遠奇點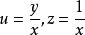 無窮遠奇點
無窮遠奇點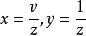 無窮遠奇點
無窮遠奇點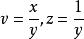 無窮遠奇點
無窮遠奇點例如對不是y軸方向的無窮遠點,可投影到平面X=1上, 與之相交於點M,在X=1上取其與球面的切點為坐標原點,u軸與Y軸平行,z軸與Z軸平行,M的坐標為(u,z)。易推出(x,y)與(u,z)的變換關係為 或 。對y軸方向的無窮遠點,則投影到平面Y=1,在其上類似地引進坐標(v,z),則易得 或 。
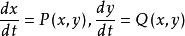 無窮遠奇點
無窮遠奇點 無窮遠奇點
無窮遠奇點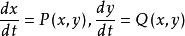 無窮遠奇點
無窮遠奇點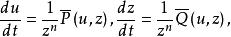 無窮遠奇點
無窮遠奇點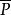 無窮遠奇點
無窮遠奇點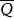 無窮遠奇點
無窮遠奇點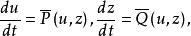 無窮遠奇點
無窮遠奇點在(u,z)坐標下, 變為 z≠0時,此方程組在X=1平面上的軌線為(x,y)平面上 的軌線的投影。而z=0恰好對應於(x,y)面上的無窮元。為消去分母上的z,設P,Q為x,y的多項式,則可將上述方程組寫成其中n為非負整數,使,為u,z的多項式且不同時含有因子z。做變換dτ=dt/z ,則化得它在z=0上的奇點u=u,z=0稱為系統的一個無窮遠奇點。
意義
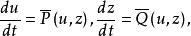 無窮遠奇點
無窮遠奇點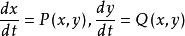 無窮遠奇點
無窮遠奇點通過對的奇點(u,0)的分析,搞清楚了它的鄰域內的軌線的性態,則它的兩個半鄰域就分別代表了在(x,y)平面上y=ux方向上的兩端無窮遠處的軌線性態。
