簡介
在計算方法中,有利用多項式對某一函式的近似逼近,計算相應的函式值。例如,在事先不知道某一函式的具體形式的情況下,只能測量得知某一些分散的函式值。例如我們不知道氣溫隨日期變化的具體函式關係,但是我們可以測量一些孤立的日期的氣溫值,並假定此氣溫隨日期變化的函式滿足某一多項式。這樣,利用已經測的數據,套用待定係數法便可以求得一個多項式函式f(x)。套用此函式就可以計算或預測其他日期的氣溫值。一般情況下,多項式的次數越多,利用的數據就越多,而預測也就越準確。
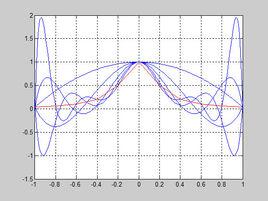
例外發生了:龍格在研究多項式插值的時候,發現有的情況下,並非取節點(日期數)越多多項式就越精確。例如f(x)=1/(1+25x^2),它的插值函式在兩個端點處發生劇烈的波動,造成較大的誤差。
程式演示
下面是MATLAB中演示對f(x)=1/(1+25x^2)插值的代碼
 龍格函式
龍格函式運行效果如右圖
圖中紅色的才是真正的函式圖形。在f(0)附近以外,插值次數越高,結果偏離越大。一般把這種次數越高而插值結果越偏離原函式的現象稱為龍格現象。所以在不熟悉曲線運動趨勢的前提下,不要輕易使用高次插值。