定義
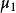 面積坐標
面積坐標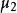 面積坐標
面積坐標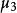 面積坐標
面積坐標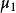 面積坐標
面積坐標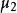 面積坐標
面積坐標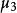 面積坐標
面積坐標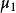 面積坐標
面積坐標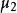 面積坐標
面積坐標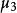 面積坐標
面積坐標平面上任取一個⊿ABC,充當坐標三角形,對於平面ABC上任意一點M,將下述三角形面積比 S⊿MBC:S⊿AMC:S⊿ABM= : : 叫做點M關於⊿ABC的 面積坐標(或 重心坐標),記作:M= ( : : )={ , , }。
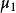 面積坐標
面積坐標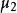 面積坐標
面積坐標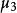 面積坐標
面積坐標註:這裡的面積 S⊿MBC,S⊿AMC,S⊿ABM都是有向面積。通常約定,頂點按逆時針方向排列的三角形面積為正,頂點按順時針方向排列的三角形面積為負,故各個坐標分量 , , 都是可正可負的。
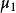 面積坐標
面積坐標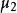 面積坐標
面積坐標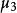 面積坐標
面積坐標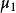 面積坐標
面積坐標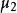 面積坐標
面積坐標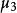 面積坐標
面積坐標由定義可知,某個點M的面積坐標既可記為 ( : : ),也可記為 (k :k :k )(k≠0)。也就是說,一個點的面積坐標記法並非唯一,他們可以相差一個非0的常數因子,因此這類坐標屬於齊次坐標,笛卡爾直角坐標不屬於齊次坐標。
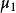 面積坐標
面積坐標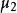 面積坐標
面積坐標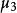 面積坐標
面積坐標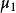 面積坐標
面積坐標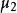 面積坐標
面積坐標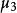 面積坐標
面積坐標當 + + =1時,面積坐標 ( : : )稱為 規範面積坐標。
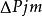 面積坐標
面積坐標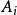 面積坐標
面積坐標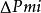 面積坐標
面積坐標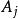 面積坐標
面積坐標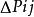 面積坐標
面積坐標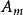 面積坐標
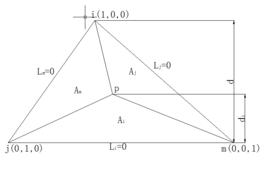
面積坐標三角形中任一點P與其3個角點相連形成3個子三角形,以原三角形邊所對應的角碼來命名此3個子三角形的面積,即 面積為 , 面積為 , 面積為 。P點的位置可有3個比值來確定,即
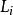 面積坐標
面積坐標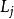 面積坐標
面積坐標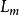 面積坐標
面積坐標P( , , )
其中
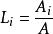 面積坐標
面積坐標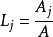 面積坐標
面積坐標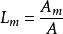 面積坐標
面積坐標A是三角形的面積,因此有
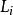 面積坐標
面積坐標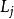 面積坐標
面積坐標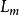 面積坐標
面積坐標+ + =1
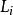 面積坐標
面積坐標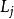 面積坐標
面積坐標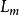 面積坐標
面積坐標稱 , , 為面積坐標。
點的面積坐標符號
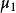 面積坐標
面積坐標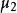 面積坐標
面積坐標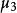 面積坐標
面積坐標設點M( : : )是規範面積坐標:
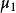 面積坐標
面積坐標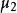 面積坐標
面積坐標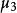 面積坐標
面積坐標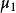 面積坐標
面積坐標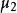 面積坐標
面積坐標 面積坐標
面積坐標1)如果點M( : : )在三角形內部,那么 、 、 屬於開區間 (0,1);
2)如果一點在三角形的邊上,至少有一個面積坐標 為 0,其餘分量位於閉區間 [0,1];
3)如果有某個坐標小於 0,則位於三角形外部。
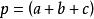 面積坐標
面積坐標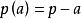 面積坐標
面積坐標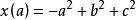 面積坐標
面積坐標例 以a、b、c分別表示⊿ABC三角A、B、C所對的邊,,,等等。
則⊿ABC的“五心”的面積坐標如下:
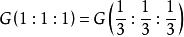 面積坐標
面積坐標重心:;
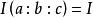 面積坐標
面積坐標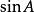 面積坐標
面積坐標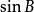 面積坐標
面積坐標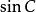 面積坐標
面積坐標內心:( : : );
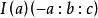 面積坐標
面積坐標旁心:,余類推;
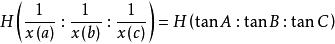 面積坐標
面積坐標垂心:;
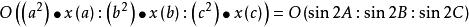 面積坐標
面積坐標外心:。