麥克斯韋-玻耳茲曼分布律
正文
全同粒子在平衡態的統計分布律。獨立的定域子體系和經典極限的離域子體系中,在平衡態下N個全同粒子分布在其單粒子任一可及能級εi(i=1,2,3,…,為單粒子能級的標號)上最可幾粒子數ni由下式確定: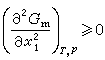

麥克斯韋-玻爾茲曼分布律可以有各種表達形式。例如,粒子在能級εi上的最可幾分布率為:


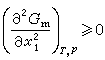
全同粒子在平衡態的統計分布律。獨立的定域子體系和經典極限的離域子體系中,在平衡態下N個全同粒子分布在其單粒子任一可及能級εi(i=1,2,3,…,為單粒子能級的標號)上最可幾粒子數ni由下式確定。
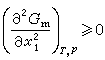



玻耳茲曼能量分布律以理想氣體在重力場中分子按狀態區間的分布為例。分子處在重力場中受重力作用,分子的空間分布是“下密上疏”。
數學定理 數據說明在某一時刻,某一特定分子的速度大小是不可預知的,且運動方向也是隨機的。但在一定的巨觀條件下,對大量氣體分子而言,它們的速度分布卻遵從一定的統計規律。麥克...
定義 歷史 內容 意義 套用路德維希·玻爾茲曼(Ludwig Edward Boltzmann,1844年2月20日—1906年9月5日),奧地利物理學家、哲學家,熱力學和統計物理...
生平簡介 人物生平 研究範圍 人物年表 社會評價路德維希·玻耳茲曼是熱力學和統計力學的奠基人之一,是一位德裔奧地利物理學家。
簡述 主要貢獻-3 能量按自由度均分原理10-4 麥克斯韋速率分布10-5 玻耳茲曼能量分布10-6 氣體分子的平均自由程和碰撞頻率10-7 氣體的輸運現象10...導體的靜電平衡條件10.1.2靜電平衡時導體上電荷的分布10.1.3...
高等教育出版社圖書 清華大學出版社圖書1 清華大學出版社圖書2 清華大學出版社圖書3一個“女性主義者”,都不會贊成普朗克的這個偏見。研究範圍玻耳茲曼推廣了J.C.麥克斯韋的分子運動理論而得到有分子勢能的麥克斯韋-玻耳茲曼分布定律...引進玻耳茲曼常量k而得出S=lnW的關係式。他又從熱力學原理導得了斯忒藩...
生平簡介 人物生平 研究範圍 人物年表 社會評價11.4玻爾茲曼分布律 11.5分子的平均自由程 11.6氣體內...基本原理和洛倫茲坐標變換式 2.2.1 狹義相對論基本原理I 2.2.2 洛倫茲坐標變換式 2.3 狹義相對論的時空觀...
圖書信息1 圖書信息2 圖書信息3 圖書信息4 圖書信息511.3分子速率的分布11.4玻爾茲曼分布律11.5分子的平均自由程11.6...基本原理和洛倫茲坐標變換式2.2.1 狹義相對論基本原理I2.2.2 洛倫茲...7.5 自感、互感和磁場的能量7.6 麥克斯韋電磁場理論簡介習題第8章...
圖書信息1 圖書信息2 圖書信息3 圖書信息4 圖書信息512.6 邁克耳遜干涉儀閱讀材料 全息照相本章提要習題第13章 光的衍射13.1 光的衍射 惠更斯—菲涅耳原理13.2 單縫夫琅禾費衍射13.3...的波動性質,薛丁格方程,原子,分子和團簇,費米統計和玻色統計,凝聚態物質...
北郵版 高教版 華科大版 高教版2 科學版