術語解釋
玻爾茲曼(L.E.Boltzmann)將麥克斯韋分布律推廣到有外力場作用的情況。在等寬的區間內,若E1>E2,則能量大的粒子數dN1小於能量小的粒子數dN2,狀態即粒子優先占據能量小的,這是玻爾茲曼分布律的一個重要結果。
經過將近一個世紀的傳播,物理學界、化學界漸漸接受了道爾頓的“原子—分子模型”,但原子、分子的確鑿證據遲遲沒有找到。恰恰此時,一股更強大的科學成就——熱力學第一、第二定律出現了。熱力學原則上解決了一切化學平衡的問題。1892年,物理化學家奧斯特瓦爾德試圖在此基礎上證明,將物理學和化學問題還原為原子或分子之間的力學關係是多餘的。他試圖將“能量”賦以實物一樣的地位,甚至要把物質還原為能量。他提出“世界上的一切現象僅僅是由於處於空間和時間中的能量變化構成的”。
在統計學中,麥克斯韋- 玻爾茲曼分布是一種特殊的機率分布,以詹姆斯·克拉克·麥克斯韋和路德維希·玻爾茲曼的名字命名。它一開始在物理中定義並使用是為了描述(特別是統計力學中描述理想氣體)在理想氣體中粒子自由移動的在一個固定容器內與其它粒子無相互作用的粒子速度,除了它們相互或與它們的熱環境交換能量與動量所產生的非常短暫的碰撞。在這種情況下粒子指的是氣態粒子(原子或分子),並且粒子系統被假定達到熱力學平衡。 在這種分布最初從麥斯威爾1960年的啟發性的基礎上衍生出來時 ,玻爾茲曼之後對這種分布的物理起源進行了大量重要調查。
 圖1
圖1粒子速度機率分布指出哪一種速度更具有可能性:粒子將具有從分布中隨機選擇的速度,並且比其它選擇方法更可能在速度範圍內。 分布取決於系統的溫度和粒子的質量。 麥克斯韋 - 波爾茲曼分布適用於經典理想氣體,這是一種理想化的實際氣體。 在實際氣體中,存在可以使其速度分布與麥克斯韋 - 波爾茲曼形式不同的各種效應(例如,范德華相互作用,渦流,相對論速度限制和量子交換相互作用)。 然而,常溫下的稀釋氣體表現得非常接近於理想的氣體,麥克斯韋速度分布對於這種氣體是非常好的近似值。 因此,它形成了動力學氣體理論的基礎,其提供了許多基本氣體性質(包括壓力和擴散)的簡化解釋。
分布函式
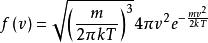 玻爾茲曼分布律
玻爾茲曼分布律麥斯威爾- 玻爾茲曼分布函式是 。
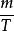 玻爾茲曼分布律
玻爾茲曼分布律 玻爾茲曼分布律
玻爾茲曼分布律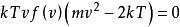 玻爾茲曼分布律
玻爾茲曼分布律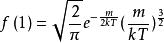 玻爾茲曼分布律
玻爾茲曼分布律在方程中, m是粒子質量, kT是玻爾茲曼常數與熱力學溫度的乘積。要注意有趣的一點是,麥克斯韋 - 波爾茲曼分布不會隨著 值即分子質量與其絕對溫度的比值而變化;數學表達式是( f( v)的導數/( m / T)的導數)= 0。該機率密度函式給出了以 附近速度求出粒子的每單位速度的機率,該方程式簡單地是具有分布參數 的麥克斯韋分布。 在機率理論中,麥克斯韋-波爾茲曼分布是具有三個自由度和尺度參數 的奇偶分布。由分布滿足的最簡單的常微分方程為: , 。
請注意,分布(函式)與機率不同。 分布(函式)代表平均數,如所有三種統計數據(Maxwell-Boltzmann,Bose-Einstein,Fermi-Dirac)。 使用達爾文 - 福勒方法的平均值,得到麥克斯韋-玻爾茲曼分布作為精確結果。
主要套用
求典型速度
平均速度,最可能的速度(眾數)和均方根可以從麥克斯韋分布的性質獲得。
最可能的速度vp是系統中任何分子(質量同等於m)最有可能擁有的速度,並且對應於f(v)的最大值或模式。 要找到它,我們需要計算導數df/dv,將其設為零並求解v:
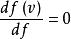 玻爾茲曼分布律
玻爾茲曼分布律。
通過此式得出:
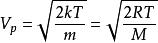 玻爾茲曼分布律
玻爾茲曼分布律,
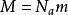 玻爾茲曼分布律
玻爾茲曼分布律其中R是氣體常數, 是物質的摩爾質量。對於室溫(300K)中的氮氣,已知 ,平均速度是速度分布的預期值:
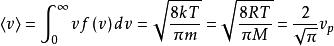 玻爾茲曼分布律
玻爾茲曼分布律。
均方根速度是二階轉速:
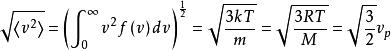 玻爾茲曼分布律
玻爾茲曼分布律。
典型速度關係如下:
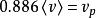 玻爾茲曼分布律
玻爾茲曼分布律;
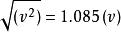 玻爾茲曼分布律
玻爾茲曼分布律;
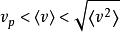 玻爾茲曼分布律
玻爾茲曼分布律;
相關推導
詹姆斯·克萊斯·麥斯威爾(James Clerk Maxwell)1860年的原始推導是基於氣動動力學理論的分子碰撞以及速度分布函式中的某些對稱性的論證;麥克斯韋還提出了一個早期的論據,認為這些分子碰撞需要平衡的趨勢。 在麥克斯韋爾(Maxwell)之後,路德維希·波茲曼(Ludwig Boltzmann)也在1872年得出了機械理論的分布,並認為由於碰撞氣體應該隨著時間的推移趨向於這種分布。 他後來(1877年)在統計熱力學的框架下再次導出了此分布。 本節的推導是按照玻爾茲曼1877的派生方式,從稱為麥斯威爾- 玻爾茲曼統計(從統計熱力學)的結果開始。 麥斯威爾- 玻爾茲曼統計量給出了在某些假設條件下給定單粒子微觀狀態中發現的平均粒子數:
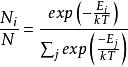 玻爾茲曼分布律
玻爾茲曼分布律⑴
在上式中:
 圖3
圖3i和j是單粒子微態的指標(或標籤)
Ni是單粒子微觀狀態i中的平均粒子數,
N是系統中的粒子總數,
Ei是microstate i的能量,
T是系統的平衡溫度,
k是波爾茲曼常數。
這個方程的假設是粒子不相互作用,而且它們是典型的; 這意味著每個粒子的狀態可以獨立於其他粒子的狀態來考慮。 另外,假定顆粒處於熱平衡狀態。 方程式⑴中的分母只是一個歸一化因子,因此Ni / N加起來為1,換句話說,它是一種分區函式(對於單粒子系統,不是整個系統的通常分區函式)。
由於速度和速度與能量有關,方程⑴可用於推導出氣體顆粒的溫度和速度之間的關係。 所需要的是發現能量中微觀狀態的密度,這是通過將動量空間分成相等大小的區域來確定的。
 圖4
圖4動量矢量分布
勢能被認為是零,所以所有能量都是動能的形式。 大量非相對論粒子的動能與動量之間的關係是:
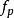 玻爾茲曼分布律
玻爾茲曼分布律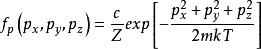 玻爾茲曼分布律
玻爾茲曼分布律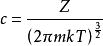 玻爾茲曼分布律
玻爾茲曼分布律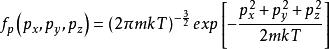 玻爾茲曼分布律
玻爾茲曼分布律⑵ ,其中P方是動量矢量P= [Px,Py,Pz]的平方。 因此,我們可以將等式(1)改寫為:⑶ ,⑶中Z是分配函式,對應於等式⑴中的分母。 這裡m是氣體的分子質量,T是熱力學溫度,k是玻爾茲曼常數。 Ni / N的這種分布與用於找到具有這些動量分量值的分子的機率密度函式 成比例,因此:⑷ 。歸一化常數c可以通過“具有一定動量的分子的機率必須為1”來確定。因此,方程⑷上的px,py和pz所有的積分必須為1。可表達為:⑸ 。將等式⑸代入等式⑷得出:⑹ 。
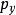 玻爾茲曼分布律
玻爾茲曼分布律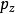 玻爾茲曼分布律
玻爾茲曼分布律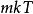 玻爾茲曼分布律
玻爾茲曼分布律該分布被認為是三個獨立的常態分配變數 , 和 的乘積,方差為 。此外,可以看出,動量的大小將以麥斯威爾- 玻爾茲曼分布分布,其中 。在氣體框架的動力學理論中,可以使用H平衡的H定理更基本地獲得麥克斯韋 - 波爾茲曼分布的動量(或等同於速度)。
能量分布
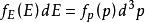 玻爾茲曼分布律
玻爾茲曼分布律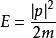 玻爾茲曼分布律
玻爾茲曼分布律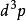 玻爾茲曼分布律
玻爾茲曼分布律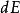 玻爾茲曼分布律
玻爾茲曼分布律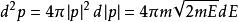 玻爾茲曼分布律
玻爾茲曼分布律能量分布是強大的:⑺,。其中是對應於能量間隔dE的動量的無窮小相空間體積。 利用能量 - 動量彌散關係的球面對稱性,可用表示為:⑻。將⑻帶入⑺中,並且使用E(能量)表達一切,我們得到如下等式:
,最終得到:
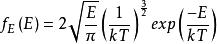 玻爾茲曼分布律
玻爾茲曼分布律⑼。
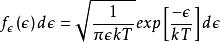 玻爾茲曼分布律
玻爾茲曼分布律由於能量與三個常態分配的動量分量的平方和成正比,所以該分布是伽馬分布; 特別是它是一個具有三個自由度的卡方分布。通過均分定理,這種能量在所有三個自由度中均勻分布,使得每個自由度的能量作為具有一個自由度的卡方分布而分布:。
在上式中ε是每自由度的能量。 在平衡狀態下,這種分布將適用於任何數量的自由度。 例如,如果某一種粒子是具有固定偶極矩的剛性質量偶極子,則它們將具有三個平移自由度和另外兩個旋轉自由度。 每個自由度的能量將根據上述具有一個自由度的卡方分布來描述,並且總能量將根據具有五個自由度的卡方分布來分布。 這對氣體比熱容理論有影響。
麥克斯韋-玻爾茲曼分布也可以通過考慮氣體作為近似ε>> k T的量子氣體來獲得。
速度矢量分布
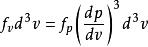 玻爾茲曼分布律
玻爾茲曼分布律通過下式確認速度 機率密度與動量機率密度函式成比例: 。
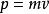 玻爾茲曼分布律
玻爾茲曼分布律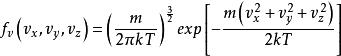 玻爾茲曼分布律
玻爾茲曼分布律通過 得到: 。
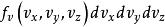 玻爾茲曼分布律
玻爾茲曼分布律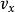 玻爾茲曼分布律
玻爾茲曼分布律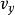 玻爾茲曼分布律
玻爾茲曼分布律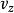 玻爾茲曼分布律
玻爾茲曼分布律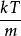 玻爾茲曼分布律
玻爾茲曼分布律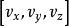 玻爾茲曼分布律
玻爾茲曼分布律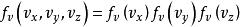 玻爾茲曼分布律
玻爾茲曼分布律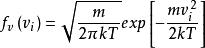 玻爾茲曼分布律
玻爾茲曼分布律上式是麥克斯韋-波爾茲曼速度分布。 關於在無窮小因子中找到具有速度的粒子的機率是: 。像動量一樣,這種分布被認為是三個獨立的常態分配變數 , , ,但是方差是 。還可以看出,矢量速度 的麥克斯韋-玻爾茲曼速度分布是三個方向中的每一個分布的產物: 。其中對於單個方向上的分布是: 。
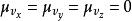 玻爾茲曼分布律
玻爾茲曼分布律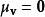 玻爾茲曼分布律
玻爾茲曼分布律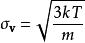 玻爾茲曼分布律
玻爾茲曼分布律速度矢量的每個分量具有平均值為 和標準差為 的常態分配,因此向量具有三維常態分配,是一種特定類型的多變數常態分配,平均值為 ,標準差為 。
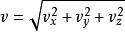 玻爾茲曼分布律
玻爾茲曼分布律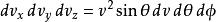 玻爾茲曼分布律
玻爾茲曼分布律速度的麥斯威爾- 玻爾茲曼分布可以立即從速度矢量的分布得到。 注意速度是 ,並且體積單位為球面坐標 ,其中φ和θ是速度矢量的“路線”(方位角)和“路徑角”(速度矢量的仰角)。 將速度的普遍機率密度函式的路線(從0到2π)和路徑角(從0到π),以速度代入矢量分量的平方和之和,得到速度分布。

