簡介
麥克斯韋關係是由J.C麥克斯韋導出的熱力學關係式，表示單相恆組成物系的溫度T、壓力p、體積v和熵S四種狀態函式之間的關係。據麥克斯韋關係式，可將難於直接測定的函式關係，便於計算。
基本方程式
麥克斯韋關係是S（熵）、T（溫度）、p（壓強）、V（體積）四個變數的偏導數關係，具體如下式：
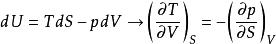麥克斯韋關係由；
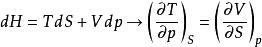麥克斯韋關係由；
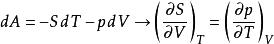麥克斯韋關係由；
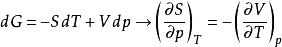麥克斯韋關係由；
由基本方程推導麥克斯韋關係式的具體過程：
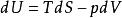麥克斯韋關係
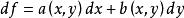麥克斯韋關係首先以為例。由於涉及的是全微分，故dS和dV的關係能用有關全微分的關係式對照。令a=T，b=-P，然後將其代入型如的全微分，可得：
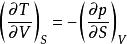麥克斯韋關係用這種簡單的方法，把這兩個初看起來似乎不能聯繫的量關聯起來。H、G、F也是狀態函式，用同樣的方法，也可得出另外三個麥克斯韋關係式：
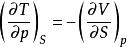麥克斯韋關係
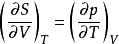麥克斯韋關係
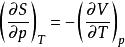麥克斯韋關係總之，通過運用數理工具，只要有完整的P- V- T關係以及C數據，利用熱力學基本方程，就可得到所有的熱力學函式U、H、S、F、G的完整信息。
對於開放系統和組成變化的系統，該原理同樣適用.因為系統自由度的增加，通常運用熱力學函式的偏導數變換的一個方便方法，即Jacobian行列式法。
麥克斯韋關係的套用
套用麥克斯韋關係可以得到以下一些有重要套用價值的關係。我們知道，系統的熵和內能等熱力學函式都不易直接測量的，它們都要通過物態方程和熱容量的實驗數據計算得到。利用麥克斯韋關係，可將這些熱力學函式用物態方程和熱容量表示出來。
（1）內能
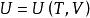麥克斯韋關係
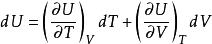麥克斯韋關係
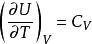麥克斯韋關係
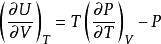麥克斯韋關係
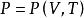麥克斯韋關係
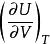麥克斯韋關係
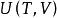麥克斯韋關係設，則。已知，由熱力學基本方程得，由麥克斯韋關係式，若已知物態，就可以求得，最後求得。
（2）焓
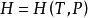麥克斯韋關係
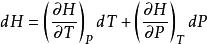麥克斯韋關係
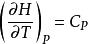麥克斯韋關係
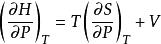麥克斯韋關係
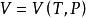麥克斯韋關係
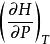麥克斯韋關係
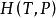麥克斯韋關係設，則。已知，由熱力學基本方程得，由麥克斯韋關係式，若已知物態，就可以求得，最後求得。
（3）熵
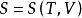麥克斯韋關係
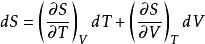麥克斯韋關係
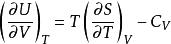麥克斯韋關係
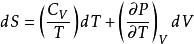麥克斯韋關係
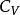麥克斯韋關係 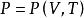麥克斯韋關係
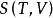麥克斯韋關係設，則。由熱力學基本方程得，由麥克斯韋關係式得。已知及物態，就可以求得。
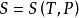麥克斯韋關係
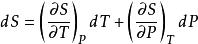麥克斯韋關係
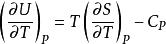麥克斯韋關係
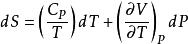麥克斯韋關係
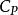麥克斯韋關係 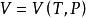麥克斯韋關係
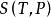麥克斯韋關係設，則。由熱力學基本方程得，由麥克斯韋關係式得。已知及物態，就可以求得。
