高聚物介電性能
在外加電場中只有束縛電荷作有限位移的材料稱電介質,一般來說,高聚物都是電介質。電介質的性能可用介電常數和介電損耗正切 tgδ兩個參數來表征。介電常數 ε是電容器中充滿該材料時的電容量與在真空時的電容量之比,真空的ε等於1,空氣的ε接近1,大多數非極性高聚物的ε為2左右,極性高聚物的ε為2~10。介電常數 表征電解質極化的巨觀參數,它與分子極化率α之間的關係由克勞修斯-莫索提公式給出:
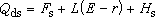
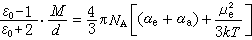 (1)
(1)
式(1)稱德拜公式,式中k為玻耳茲曼常數;T為熱力學溫度。只有電子極化和原子極化的非極性高聚物可通過麥克斯韋關係用折射率n表示:ε=n2,式中ε和n應在同一頻率下測量。極性高聚物由於偶極極化,ε的實測值偏離n2較大。
介電損耗正切 也稱介電損耗因子,tgδ是電介質在交變電場中損耗能量與貯存能量之比。由於電介質、基團或偶極的取向運動存在著阻力,使得極化滯後於電場的變化,其滯後相角δ的正切tgδ正比於材料在交變電場中能量的損耗。高聚物是具有低介電常數和低介電損耗的優良絕緣材料,非極性高聚物的tgδ可小於1×10-4,極性高聚物的tgδ為5×10-3~1×10-1。電介質在交變電場中能量的損耗與交變電場的頻率f以及tgδ成正比,因此tgδ高的聚合物由於能將較多的電能轉變為熱能,所以它適合於高頻焊接或高頻加熱,但不適合作高頻絕緣材料。
複數介電常數 在交變電場中的介電性能要用複數介電常數ε*來描述:
ε*=ε′-iε″
式中ε′為實數部分,ε″為虛數部分,因此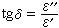 。
。
介電性能與溫度 高聚物的介電性能有顯著的頻率和溫度依賴性。具有單一鬆弛時間的電介質(實際上高聚物鬆弛時間分布很寬,是個譜)的介電性能的頻率依賴性由德拜色散方程給出:
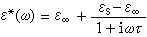 (2)
(2) 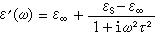 (3)
(3) 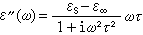 (4)
(4)
式(2)、(3)、(4)中ε∞和εS分別為色散區兩側高頻和低頻區的介電常數,稱為未鬆弛和已鬆弛介電常數;ω 為角頻率;τ為鬆弛時間。
高聚物介電性能與溫度的關係是通過鬆弛時間 τ與溫度的依賴性相聯繫的,即:
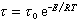
式中τ0為常數;E為活化能;R為氣體常數;T為絕對溫度。
介電色散 由式(3)、(4)可知,ε′和ε″為lgωτ的函式,當ωτ=1時,ε′發生驟變而ε″出現峰值,這種現象稱為介電色散。高分子介電色散是基團和鏈段松弛過程的表現,因此,高聚物的介電性能溫度譜或頻率譜是研究高聚物轉變和鬆弛以及分子運動的重要方法之一。