簡介
在機率論和統計學中， 馬可夫決策過程（MDPs）提供了一個數學架構模型，用於面對部分隨機，部分可由決策者控制的狀態下，如何進行決策，以俄羅斯數學家安德雷·馬爾可夫的名字命名。在經由動態規劃與強化學習以解決最佳化問題的研究領域中，馬可夫判決過程是一個有用的工具。
馬爾可夫過程在機率論和統計學方面皆有影響。一個通過不相關的自變數定義的隨機過程，並（從數學上）體現出馬爾可夫性質，以具有此性質為依據可推斷出任何馬爾可夫過程。實際套用中更為重要的是，使用具有馬爾可夫性質這個假設來建立模型。在建模領域，具有馬爾可夫性質的假設是向隨機過程模型中引入統計相關性的同時，當分支增多時，允許相關性下降的少有幾種簡單的方式。
馬爾可夫判決過程是指決策者周期地或連續地觀察具有馬爾可夫性的隨機動態系統，序貫地作出決策。即根據每個時刻觀察到的狀態，從可用的行動集合中選用一個行動作出決策，系統下一步（未來）的狀態是隨機的，並且其狀態轉移機率具有馬爾可夫性。決策者根據新觀察到的狀態，再作新的決策，依此反覆地進行。馬爾可夫性是指一個隨機過程未來發展的機率規律與觀察之前的歷史無關的性質。馬爾可夫性又可簡單敘述為狀態轉移機率的無後效性。狀態轉移機率具有馬爾可夫性的隨機過程即為馬爾可夫過程。馬爾可夫判決過程又可看作隨機對策的特殊情形，在這種隨機對策中對策的一方是無意志的。馬爾可夫判決過程還可作為馬爾可夫型隨機最優控制，其決策變數就是控制變數。
發展概況
50年代，R.貝爾曼研究動態規劃時和L.S.沙普利研究隨機對策時已出現馬爾可夫判決過程的基本思想。R.A.霍華德(1960)和D.布萊克韋爾(1962)等人的研究工作奠定了馬爾可夫判決過程的理論基礎。1965年，布萊克韋爾關於一般狀態空間的研究和E.B.丁金關於非時齊（非時間平穩性）的研究，推動了這一理論的發展。1960年以來，馬爾可夫判決過程理論得到迅速發展，套用領域不斷擴大。凡是以馬爾可夫過程作為數學模型的問題，只要能引入決策和效用結構，均可套用這種理論。
定義
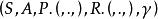馬爾可夫判決過程馬爾可夫判決過程是一個五元組 ，其中 ，
馬爾可夫判決過程1) 是一組有限的狀態；
馬爾可夫判決過程
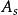馬爾可夫判決過程
馬爾可夫判決過程2) 是一組有限的行為（或者， 是從狀態可用的有限的一組行動 ）；
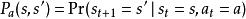馬爾可夫判決過程
馬爾可夫判決過程 馬爾可夫判決過程
馬爾可夫判決過程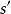
馬爾可夫判決過程
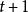馬爾可夫判決過程3) 是行動的機率 在狀態 在時間 會導致狀態 在時間 ；
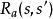馬爾可夫判決過程4) 是從國家轉型後得到的直接獎勵（或期望的直接獎勵）；
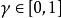馬爾可夫判決過程5) 是折現係數子，代表未來獎勵與現在獎勵之間的重要差異。
馬爾可夫判決過程 馬爾可夫判決過程（註：馬爾可夫決策過程的理論並沒有說明這一點 要么 是有限的，但是下面的基本算法假設它們是有限的）。
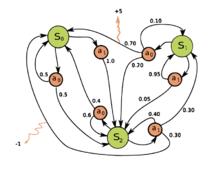馬爾可夫判決過程圖1表示具有三個狀態（綠色圓圈）和兩個動作（橙色圓圈）的簡單MDP的示例。
描述
馬爾可夫判決過程
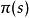馬爾可夫判決過程MDP的核心問題是為決策者找到一個“判決”：一個功能 指：決策者什麼時候會選擇行動 。一旦馬爾可夫決策過程以這種方式與政策相結合，就可以解決每個狀態的行為，並且產生的組合行為就像一個馬爾可夫鏈。
馬爾可夫判決過程
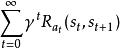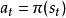馬爾可夫判決過程
馬爾可夫判決過程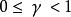
馬爾可夫判決過程
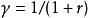馬爾可夫判決過程
馬爾可夫判決過程 馬爾可夫判決過程目標是選擇一項判決 這將最大化隨機獎勵的一些累積函式，通常是在可能無限的時間範圍內的期望折扣總和： ，這裡選擇的地方。 是折扣因素和滿足 。例如， 當折扣率為r時， 通常接近1。
馬爾可夫判決過程由於馬爾可夫屬性，這個特定問題的最優策略確實可以寫成一個函式 只有，如上所述。
策略指標
馬爾可夫判決過程
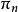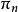馬爾可夫判決過程 馬爾可夫判決過程
馬爾可夫判決過程策略是提供給決策者在各個時刻選取行動的規則，記作 ，其中 是時刻n選取行動的規則。從理論上來說，為了在大範圍尋求最優策略 ，最好根據時刻 以前的歷史，甚至是隨機地選擇最優策略。但為了便於套用，常採用既不依賴於歷史、又不依賴於時間的策略，甚至可以採用確定性平穩策略。
馬爾可夫判決過程
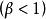馬爾可夫判決過程衡量策略優劣的常用指標有折扣指標和平均指標。折扣指標是指長期折扣〔把 時刻的單位收益折合成0時刻的單位收益的 倍〕期望總報酬；平均指標是指單位時間的平均期望報酬。
馬爾可夫判決過程採用折扣指標的馬爾可夫決策過程稱為 折扣模型。業已證明：若一個策略是 折扣最優的，則初始時刻的決策規則所構成的平穩策略對同一也是折扣最優的，而且它還可以分解為若干個確定性平穩策略，它們對同一β都是最優的，已有計算這種策略的算法。
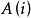馬爾可夫判決過程
馬爾可夫判決過程 馬爾可夫判決過程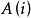 馬爾可夫判決過程採用平均指標的馬爾可夫決策過程稱為 平均模型。已證明：當狀態空間 和行動集 均為有限集時，對於平均指標存在最優的確定性平穩策略；當 和 不是有限的情況,必須增加條件，才有最優的確定性平穩策略。計算這種策略的算法也已研製出來。
擴展
1.約束馬爾可夫判決過程
約束馬爾可夫決策過程（CMDPs）是馬爾可夫決策過程（MDPs）的擴展。MDPs和CMDPs有三個基本的區別。
1）套用時一個動作而不是一個動作需要多個成本；
2）CMDP只能通過線性程式來解決，動態編程不起作用；
3）最終的判決取決於開始的狀態。
CMDP有很多套用。它最近被用在機器人的運動規劃場景中。
2.模糊馬爾可夫判決過程（FMDPs）
在MDPs中，最優策略是使未來獎勵的機率加權總和最大化的策略。因此，最優策略由幾個屬於一組有限行為的動作組成。在模糊馬爾可夫判決過程（FMDPs）中，首先，價值函式被計算為規則的MDPs（即具有有限的一組行動）；那么，這個策略是通過一個模糊推理系統來提取的 。換句話說，價值函式被用作模糊推理系統的輸入，策略是模糊推理系統的輸出。
