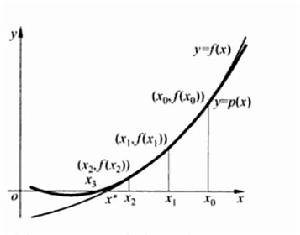
y=f(x)的零點x'來說,假設已經得到互異的三個點x0,x1,x2處的函式值f(x0),f(x1),f(x2),那么可以 經過平面上的三個點(x0,f(x0)),(x1,f(x1))以及(x2,f(x2))作為拋物線,記為y=p(x)(圖中較粗的那條曲線),並把拋物線y=p(x)與x軸的交點x3作為f(x)=0的近似解。接下來再經過(x1,f(x1)),(x2,f(x2))以及
(x3,f(x3))作為拋物線……從而形成一個算法,算法的關鍵是求拋物線與x軸的交點。
假設過(x0,f(x0)), (x1,f(x1))以及(x2,f(x2))這三個點的拋物線方程為
y=a(x-x2) ^2+b(x-x2)+c ************************************ (1)
依次用(x0,f(x0)),(x1,f(x1))以及(x2,f(x2))分別代入(1)式,得
f(x0)= a(x0-x2) ^2+b(x0-x2)+c ****************************(2)
f(x1)= a(x1-x2) ^2+b(x1-x2)+c *************************** (3)
f(x2)= a(x2-x2) ^2+b(x2-x2)+c *****************************(4)
由(4)式可得c=f(x2),分別代入到(2)(3)中,整理後得
a(x0-x2) ^2+b(x0-x2)+c=f(x0)-f(x2)********************** (5)
a(x1-x2) ^2+b(x1-x2)+c=f(x1)-f(x2)********************** (6)
為了把上面的方程組(5)(6)的解更有規律性,令
h0= x1-x0
h1= x2-x1
q0=[f(x1)-f(x0)]/h0 *************************************(7)
q1=[f(x2)-f(x1)]/h1
把上面的定義的方程組分別代入(5)(6)中,整理後可得
a=(q1-q0)/(h1+h0)
b=q1+ah1 ***********************************************(8)
再在(1)式中令y=0,利用求根公式解關於x-x2的方程可以得到
x1-x2=[(-b)+√(b ^2-4ac)]/2a************************* (9)
x1= x2 +[(-b)+√(b ^2-4ac)]/2a************************ (10)
由圖可以看出,如果得到了插值拋物線的兩個零點,應該取與x2更靠近的哪一個最為問題的近似解。利用一元二次方程的求根的計算方法,可以得到
x= x2 – 2c/[(b+sign(b)+ √(b ^2-4ac)] **************(11)
上面的(11)式可以用來求下一個疊代點,其中a,b,c可以利用(7)式和(9)式得到,從而利用Muller方法求函式零點的關鍵問題得到解決。
