布倫特（Brent）方法初步感覺有些小題大做，仔細分析又不無道理。
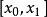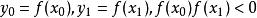布倫特法
布倫特法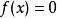
布倫特法
布倫特法假如知道f(x)的零點x’在一個不太大的區間 內，而且已知 在區間的端點處的函式值 ,以及 在（x0,x1）內的近似解x=x2和f(x2)，接下來利用這已知的三個點以及它們所對應的函式值作插值拋物線。與Muller方法不同的是，把
x0 ，x1 ，x2 與f(x0), f(x1), f(x2)的對應關係反過來用，相當於用y0 ，y1 ，y2 替代方程組
f(x0)= a(x0-x2) ^2+b(x0-x2)+c **************** (1)
f(x1)= a(x1-x2) ^2+b(x1-x2)+c **************** (2)
f(x2)= a(x2-x2) ^2+b(x2-x2)+c **************** (3)
中的x0 ，x1 ，x2 ，而方程組的常數項f(x0), f(x1), f(x2) 則用這裡的x0 ，x1 ，x2替換。所以對應的插值拋物線的一般形式為
x= a(y-y2) ^2+b(y-y2)+c **************** (4)
x0= a(y0-y2) ^2+b(y0-y2)+c **************** (5)
x1= a(y1-y2) ^2+b(y1-y2)+c **************** (6)
x2= a(y2-y2) ^2+b(y2-y2)+c **************** (7)
由（5）（6）（7）式可以得c=x2,利用Muller方法，可以寫成a,b 的表達式。
在（4）中令y=0,可以得到下一個近似點為
X=x2+(ay2 ^2+by2) **************** (8)
其中ay2 ^2+by2相當於校正項。
Brent方法的下一個規則是，如果得到的x仍然在區間[x0,x1]內，則用x2根據f(x2)
的符號替換x0或x1 ，用x替換x2；如果所得到的x不在區間[x0,x1]內，則暫時放棄反拋物線插值法，繼續用二分法或試位法。
實際上，我們可以利用二分法所得到函式順便採用反插值方法試探一下，看能否撿到一些便宜。
在這種平常心態下，我們也可以得到類似的效果，而且方法還簡單得多。
