非齊次泊松過程

非齊次泊松過程(non-homogeneous Poisson process)【1 】是泊松過程一個推廣.如果允許泊松過程的定義中時刻t的來到強度（或速率）是t的函式λ(t)，就得到非齊次泊松過程.

確切地說，如果計數過程{X(t) ,t >= 0)滿足以下條件:

1.X(0) = 0;

2.X(t)是獨立增量的過程；

3.P{X(t+h) - X(t) = 1} = λ(t)h + o(h),

P{X(t+h) - X(t) >= 2} = o(h).

則稱計數過程{X(t),t>=0}為具有跳躍強度函式λ(t)的非齊次泊松過程。

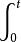非齊次泊松過程

非齊次泊松過程的均值函式為m(t) = λ(s) ds.

非齊次泊松過程的機率分布由下面定理給出：

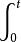非齊次泊松過程

定理 設{X(t),t>=0}是具有均值函式m(t) = λ(s) ds的非齊次泊松過程，則有

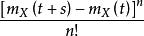非齊次泊松過程

P{X(t+s) - X(t) = n}=exp{-[m(t+s)-m(t)]},n>=0,

非齊次泊松過程

或P{X(t) = n}=exp{-m(t)},n>=0.[2 ]