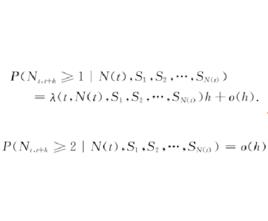自激點過程的定義
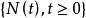 自激點過程
自激點過程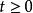 自激點過程
自激點過程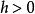 自激點過程
自激點過程在數學上,自激點過程被定義為滿足下述條件的計數過程:對任意實數和,
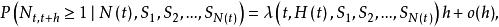 自激點過程
自激點過程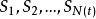 自激點過程
自激點過程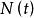 自激點過程
自激點過程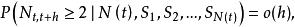 自激點過程
自激點過程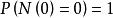 自激點過程
自激點過程其中依次是過程的第一,第二,……,第個點發生時刻。在某些文獻的定義中還加上有序性條和對初始狀態的規定:。
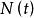 自激點過程
自激點過程注意自激點過程的強度λ不僅隨時間t變化,而且還是過程的現實ω的函式,即強度本身是一隨機過程,但它受點過程自身的演化制約 。
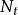 自激點過程
自激點過程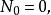 自激點過程
自激點過程如果計數過程 滿足: 且對於小時間h有
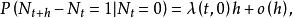 自激點過程
自激點過程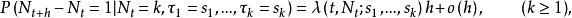 自激點過程
自激點過程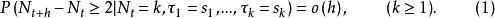 自激點過程
自激點過程則稱為 自激點過程,而隨機過程
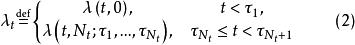 自激點過程
自激點過程稱為其 強度過程 。
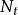 自激點過程
自激點過程自激點過程 稱為m-記憶的,如果
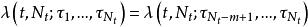 自激點過程
自激點過程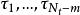 自激點過程
自激點過程即強度過程只依賴最近發生的m個事件的時刻,而與 無關。
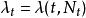 自激點過程
自激點過程最簡單的是 的情形,這是無記憶(0-記憶)的自激點過程情形,即下面的定義。
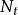 自激點過程
自激點過程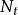 自激點過程
自激點過程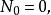 自激點過程
自激點過程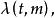 自激點過程
自激點過程定義1計數過程 稱為 無記憶的自激點過程,如果 滿足: 且存在正值函式 使對於小的h有
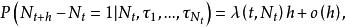 自激點過程
自激點過程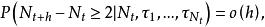 自激點過程
自激點過程由此可見,無記憶的自激點過程是條件非時齊Poisson過程。
 自激點過程
自激點過程 自激點過程
自激點過程 自激點過程
自激點過程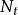 自激點過程
自激點過程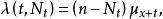 自激點過程
自激點過程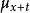 自激點過程
自激點過程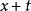 自激點過程
自激點過程例1年齡 的 個人的群體在時刻 以前的死亡人數(死亡計數過程) 可以用無記憶的自激點過程建模,其強度過程為 其中 是年齡為 的死亡率,
無記憶的自激點過程的有限維分布
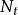 自激點過程
自激點過程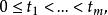 自激點過程
自激點過程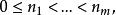 自激點過程
自激點過程無記憶的自激點過程 在有限個時刻上的聯合分布為: 對於 整數
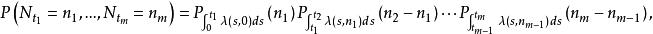 自激點過程
自激點過程其中
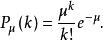 自激點過程
自激點過程自激點過程的條件強度過程
定義2
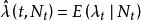 自激點過程
自激點過程稱為自激點過程的 條件強度過程。
於是,對於自激點過程有
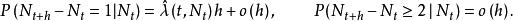 自激點過程
自激點過程自激點過程的絕對機率
仿照初等機率論中Poisson過程的絕對機率的推導,可以得到
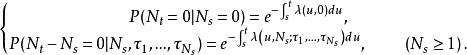 自激點過程
自激點過程同樣仿照初等機率論中Poisson過程的絕對機率的推導,我們得到下面的結論。
命題1 自激點過程的絕對機率滿足如下的(常微分方程組)
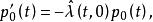 自激點過程
自激點過程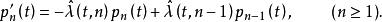 自激點過程
自激點過程這是一個非時齊的單側純生過程,可以用歸納法求得其解為
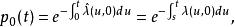 自激點過程
自激點過程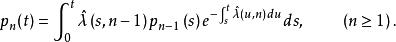 自激點過程
自激點過程