定義
所謂非負數,是指零和正實數。非負數的性質在解題中頗有用處,常見的非負數有三種:實數的偶次冪、實數的絕對值和算術根。
類型
實數的偶次冪是非負數
 非負數
非負數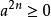 非負數
非負數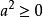 非負數
非負數若 是任意實數,則 (n為正整數),特別地,當n=1時,有 。
實數的絕對值是非負數
 非負數
非負數 非負數
非負數若是實數.則
性質:絕對值最小的實數是零。
算術根及其中的被開方數
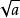 非負數
非負數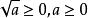 非負數
非負數是算術根,則 。
 非負數
非負數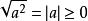 非負數
非負數性質:一個正實數的算術根是非負數,若是實數,則。
三個實數平方和與兩兩積之和的差
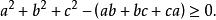 非負數
非負數非負數的其他性質
①數軸上,原點和原點右邊的點表示的數都是非負數。
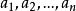 非負數
非負數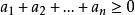 非負數
非負數②有限個非負數的和仍為非負數,即若 為非負數,則 。
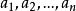 非負數
非負數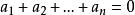 非負數
非負數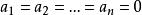 非負數
非負數③有限個非負數的和為零,那么每一個加數也必為零,即若 為非負數,且 ,則必有 。
在利用非負數解決問題的過程中,這條性質使用得最多。
④非負數的積和商(除數不為零)仍為非負數。
⑤最小非負數為零,沒有最大的非負數。
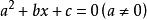 非負數
非負數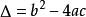 非負數
非負數⑥一元二次方程 有實數根的充要條件是判別式 為非負數。
套用非負數解決問題的關鍵在於能否識別並揭示出題目中的非負數,正確運用非負數向有關概念及其性質,巧妙地進行相應關係的轉化,從而使問題得到解決。
非負數的套用
利用非負數求代數式的值
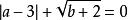 非負數
非負數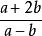 非負數
非負數例1 已知.求的值。
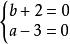 非負數
非負數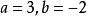 非負數
非負數講解 由題意,解得。
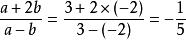 非負數
非負數代入代數式得。
評註 本題利用絕對值和根式的 非負數性質求解,比較容易簡單。
利用非負數求最值
 非負數
非負數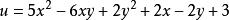 非負數
非負數 非負數
非負數例2 已知為實數,求的最小值和取得最小值時的的值。
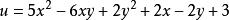 非負數
非負數講解
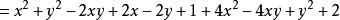 非負數
非負數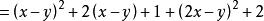 非負數
非負數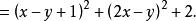 非負數
非負數 非負數
非負數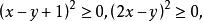 非負數
非負數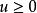 非負數
非負數因為為實數,所以,所以。
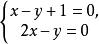 非負數
非負數 非負數
非負數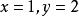 非負數
非負數所以當 時,有最小值2,此時。
評註 利用非負數求最值,需對問題條件進行變形,寫成非負數形式是關鍵。
利用非負數求方程的根或個數
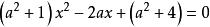 非負數
非負數例3 確定方程的實數根的個數。
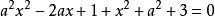 非負數
非負數講解 (方法一) 將原方程化為,
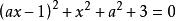 非負數
非負數即,
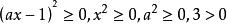 非負數
非負數對於任意實數x,均有,
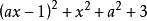 非負數
非負數所以恆大於0,
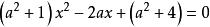 非負數
非負數故無實根。
(方法二) 利用判別式判斷。
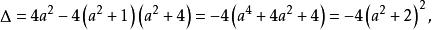 非負數
非負數因為判別式小於零,所以無解。
評註 本題確定方程根的個數,首先判斷方程類型尤其重要。

