引入
集合”一詞與我們日常熟悉的“整體”、“一類”“一群”等詞語的意義相近。例如，“數學書的全體”、“地球上人的全體”“所有文具的全體”等都可分別看成一些“對象”的集合。
我們看到的、聽到的、聞到的、觸摸到的、想到的各種各樣的事物或一些抽象的符號，都可以看作 對象.一般地，把一些能夠 確定的 不同的對象看成一個整體，就說這個整體是由這些對象的全體構成的 集合（或 集）。
集合是數學中的一個基本概念，我們先說明下，例如，一個書櫃中的書構成一個集合，一間教室里的學生構成一個集合，全體實數構成一個集合。一般的，所謂 集合（簡稱“集”） 是指具有某種特定性質的事物的總體，組成這個集合的事物稱為該集合的元素（簡稱”元“）。通常用大寫字母表示集合，小寫字母表示元素。比如a∈A，即元素a屬於集合A。
定義
子集是集合論的基本概念之一，指兩個具有包含關係的集合中的被包含者。
子集
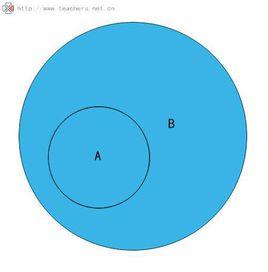
定義1 設A，B是兩個集合，如果集合A中任意一個元素都是集合B的元素，則稱A是B的 子集，記作A ⊆B或B ⊆A，讀作“A含於B”或“B包含A”.
A是B的子集可用符號表述為
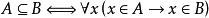非空真子集或
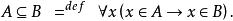非空真子集真子集
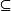非空真子集
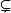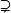非空真子集
非空真子集定義2 若A是B的一個子集，並且集合B至少有一個元素不在集合A中，即A B且A≠B，則稱A為B的 真子集，同時稱B為A的真擴集，記為A B或B A，讀作“A真含於B”或“B真包含A”.
A是B的真子集可用符號表述為
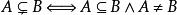非空真子集或
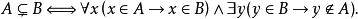非空真子集例如，B={a、b、c、d、e}真包含A={a、b、c}，即A是B的一個真子集。
註：不含任何元素的集合稱為空集， 空集是任何集合的子集，且空集是任何非空子集的真子集。
非空真子集
定義3 若A是B的一個真子集，且A不是空集，則稱A為B的 非空真子集。
註：1.在一個集合的所有子集中，除空集和它本身之外的子集叫做非空真子集。
2.若A中有n個元素，則A有2^n個子集，（2^n-1）個真子集，（2^n-2）個非空真子集。
舉例
例如，{1，2}的子集有{1}，{2} ，{1，2}，∅，那么，它的非空真子集就是{1}，{2}。
