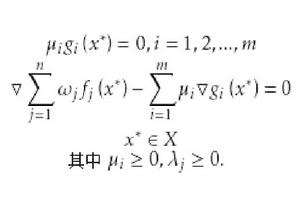基本介紹
一般來說多目標規劃問題(VP)的絕對最優解是不存在的。當絕對最優解不存在時,需要引入新的“解”的概念—— 非劣解( non-inferior solution),又稱 非控解(non-dominance solution)、 有效解(efficient solution)、 巴列托最優解(Pareto-optimal solution)、錐最優解( cone-optimal solution)。
 非劣解
非劣解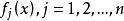 非劣解
非劣解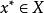 非劣解
非劣解 非劣解
非劣解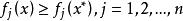 非劣解
非劣解 非劣解
非劣解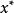 非劣解
非劣解非劣解 設 為多目標決策問題向量目標函式,其分量 均越大越優。對 ,若在X中不存在 使 ,且至少對一個 嚴格不等式成立,則稱 為向量最佳化問題的 非劣解。
所謂非劣解是指這樣的方案(記作A),在可行解集中再也找不到另一方案B,方案B的各目標函式值(屬性值)都不劣於方案A的相應目標值,而且B至少有一個目標比方案A優。
根據決策人的偏好結構從非劣解集中選出的決策人最滿意的解叫 最佳調和解(Best Compromise Solution)。
產生非劣解的主要方法
下面,簡單介紹三種產生非劣解的主要方法。
K-T條件
1) 純量最佳化問題的K-T條件
非線性規劃
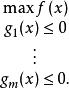 非劣解
非劣解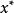 非劣解
非劣解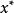 非劣解
非劣解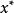 非劣解
非劣解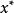 非劣解
非劣解設 滿足約束條件,如果梯度向量對於 在下標集上(起作用約束)是線性獨立的,則稱 是正則點(對 起作用的約束條件的梯度是線性獨立的)。
K-T條件:
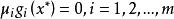 非劣解
非劣解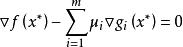 非劣解
非劣解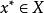 非劣解
非劣解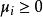 非劣解
非劣解其中 .
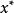 非劣解
非劣解 非劣解
非劣解它是最優解 的一個必要條件,但不一定充分。如果 是凹函式,可行空間X是凸域,則K-T條件也是充分條件。
2) 向量最佳化問題的K-T條件
向量最佳化問題存在非劣解的必要條件:
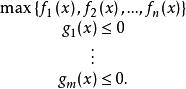 非劣解
非劣解K-T條件:
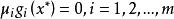 非劣解
非劣解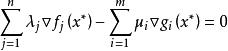 非劣解
非劣解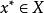 非劣解
非劣解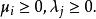 非劣解
非劣解其中
有了向量最佳化問題的非劣解的K-T條件,即可介紹非劣解的產生方法。最常用的方法有加權法和約束法。這些方法的公共特點是把向量最佳化問題轉為純量最佳化問題。
加權法
加權法就是通過對目標函式的加權,直接利用K-T條件推出非劣解。
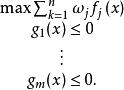 非劣解
非劣解K-T條件:
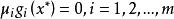 非劣解
非劣解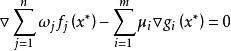 非劣解
非劣解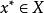 非劣解
非劣解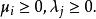 非劣解
非劣解其中
由於
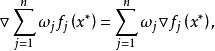 非劣解
非劣解可知
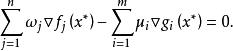 非劣解
非劣解加權的純量最佳化問題的最優解和原來的向量最佳化問題的非劣解有相同的K-T必要條件。
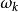 非劣解
非劣解可以證明:只有當權 都嚴格為正時,才能保證加權的純量問題的最優解是原來的向量最佳化問題的非劣解。
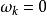 非劣解
非劣解如果有一個或多個 ,則純量最佳化問題找到的最優解有可能不是唯一的,在這些最優解中,有的解可能是原來的向量最佳化問題的劣解。
約束法
約束法可以由非劣解的K-T條件直接導出。
一般情況:
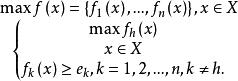 非劣解
非劣解