較多有效解

概念

較多有效解(majorly efficient solution)是多目標規劃的基本概念之一。是使多目標規劃問題中的較多個目標函式為非劣的解。對於多目標規劃問題(VMP)，設x～∈X，若不存在x∈X使得f(x)≤f(x～)(k=1，2，…，m)中至少有：

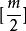較多有效解

個成立，並且其中至少有一為嚴格不等式，則稱x～是(VMP)的較多有效解。多目標規劃問題(VMP)的較多有效解必是它的有效解和較多最優解。

有效解

亦稱帕雷托有效解或帕雷托解。多目標規劃的基本概念之一。對於多目標規劃問題(VMP)，設x～∈X，若不存在x∈X使得f(x)≤f(x～)(k=1，2，…，m)，並且其中至少有一為嚴格不等式，則稱x～是(VMP)的有效解。多目標規劃問題(VMP)的有效解必是它的弱有效解。

最優解

通常定義為不犧牲任何總目標和各分目標的條件下，技術上能夠達到的最好的解。它表示所有的總目標和分目標都可以達到的理想的解。而實際上這樣的解是很少存在的。工程問題固有的內在因素總是包含各種矛盾的，由於科學水平的限制，很多設計因素和系統的約束還不是很了解;許多判別準則。例如： 社會上的相互關係、生活的質量、生態學，以及興趣、愛好等等，是不容易確定的，更不容易定量化。而工程系統的設計問題或規劃問題中勞動力、設備、財力以及時間總是有限的。所以，最最佳化過程只是產生一個在設計和工藝約束條件下所能達到的“最令人滿意的解”。

數學規劃的基本概念之一。指在數學規劃問題中，使目標函式取最小值(對極大化問題取最大值)的可行解。使目標函式取最小值的可行解稱為極小解(點)，使其取最大值的可行解稱為極大解(點)。極小解(點)或極大解(點)均稱為最優解(點)。相應地，目標函式的最小值或最大值稱為最優值。有時，也將最優解(點)和最優值一起稱為相應數學規劃問題的最優解。

多目標規劃

多目標規劃是數學規劃的一個分支。研究多於一個的目標函式在給定區域上的最最佳化。又稱多目標最最佳化。通常記為 MOP(multi-objective programming)。

多目標規劃的概念是 1961年由美國數學家查爾斯和庫柏首先提出的。多目標最最佳化思想，最早是在1896年由法國經濟學家V.帕雷托提出來的。他從政治經濟學的角度考慮把本質上是不可比較的許多目標化成單個目標的最 最佳化問題，從而涉及了多目標規劃問題和多目標的概念。

1947年，J.馮·諾伊曼和O.莫根施特恩從對策論的角度提出了有多個決策者在彼此有矛盾的情況下的多目標問題。1951年，T.C.庫普曼斯從生產和分配的活動中提出多目標最最佳化問題，引入有效解的概念，並得到一些基本結果。同年，H.W.庫恩和 A.W.塔克爾從研究數學規劃的角度提出向量極值問題，引入庫恩-塔克爾有效解概念，並研究了它的必要和充分條件。1963年，L.A.扎德從控制論方面 提出多指標最最佳化問題，也給出了一些基本結果。1968年，A.M.日夫里翁為了排除變態的有效解，引進了真有效解概念，並得到了有關的結果。自70年代 以來，多目標規劃的研究越來越受到人們的重視。至今關於多目標最優解尚無一種完全令人滿意的定義，所以在理論上多目標規劃仍處於發展階段。

目標函式

目標函式f(x)就是用設計變數來表示的所追求的目標形式，所以目標函式就是設計變數的函式，是一個標量。從工程意義講，目標函式是系統的性能標準，比如，一個結構的最輕重量、最低造價、最合理形式；一件產品的最短生產時間、最小能量消耗；一個實驗的最佳配方等等，建立目標函式的過程就是尋找設計變數與目標的關係的過程，目標函式和設計變數的關係可用曲線、曲面或超曲面表示。

一個工程設計問題 ，常有許多可行的設計方案 ，最最佳化設計的任務是要找出其中最優的一個方案。評價最優方案的標準應是在設計中能最好地反映該項設計所要追求的某些特定目標。通常 ，這些目標可以表示成設計變數的數學函式 ，這種函式稱為目標函式。