定義
對於多目標規劃問題
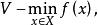 較多最優解
較多最優解引進它的由較多序定義的兩個解,並且討論這些解的有關基本性質,(VMP)的可達目標集
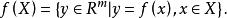 較多最優解
較多最優解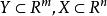 較多最優解
較多最優解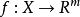 較多最優解
較多最優解定義1 設 和XcR“是非空集合, 。
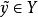 較多最優解
較多最優解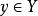 較多最優解
較多最優解(1) 若 ,並且不存在 使得
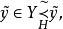 較多最優解
較多最優解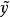 較多最優解
較多最優解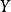 較多最優解
較多最優解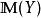 較多最優解
較多最優解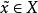 較多最優解
較多最優解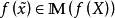 較多最優解
較多最優解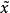 較多最優解
較多最優解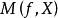 較多最優解
較多最優解則稱 是集合 的 較多有效點。Y的所有較多有效點組成的集合記作 ,若 並且 ,則稱 是多目標規劃問題(VMP)的 較多有效解。(VMP)的所有較多有效解組成的集合記作 。
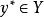 較多最優解
較多最優解(2) 若 ,並且
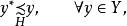 較多最優解
較多最優解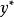 較多最優解
較多最優解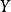 較多最優解
較多最優解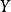 較多最優解
較多最優解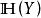 較多最優解
較多最優解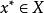 較多最優解
較多最優解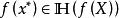 較多最優解
較多最優解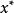 較多最優解
較多最優解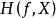 較多最優解
較多最優解則稱 是集合 的 較多最優點, 的所有較多最優點組成的集合記作 。若 並且 ,則稱 是多目標規劃問題(VMP)的 較多最優解。(VMP)的所有較多最優解組成的集合記作 。
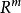 較多最優解
較多最優解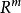 較多最優解
較多最優解中集合的較多有效點是在較多序意義下該集合中不存在比它更好點的點,從而(VMP)的較多有效解即是在較多序意義下它的約束集中不存在比它更好解的解。(VMP)的較多有效解就是對於它的向量目標中的較多個目標而言是非劣的解。 中集合的較多最優點是在較多序意義下該集合中的最好點,(VMP)的較多最優解即在較多序意義下它的約束集中的最好解。(VMP)的較多最優解也即對其向量目標中較多個目標而言是最優的解。
相關定理
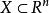 較多最優解
較多最優解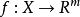 較多最優解
較多最優解定理1 設 是非空集合, 。
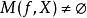 較多最優解
較多最優解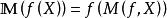 較多最優解
較多最優解(1)若 ,則 。
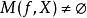 較多最優解
較多最優解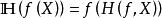 較多最優解
較多最優解(2)若 ,則 。
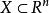 較多最優解
較多最優解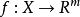 較多最優解
較多最優解定理2 設 是非空集合, ,記
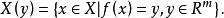 較多最優解
較多最優解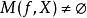 較多最優解
較多最優解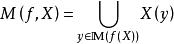 較多最優解
較多最優解(1) 若 ,則 。
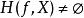 較多最優解
較多最優解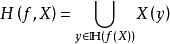 較多最優解
較多最優解(2) 若 ,則 。
下面給出較多有效點(解)和較多最優點(解)的一個充要條件。
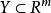 較多最優解
較多最優解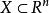 較多最優解
較多最優解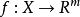 較多最優解
較多最優解定理3設 和 是非空集合, 。
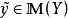 較多最優解
較多最優解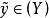 較多最優解
較多最優解(1) 若且唯若 並且
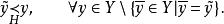 較多最優解
較多最優解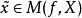 較多最優解
較多最優解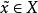 較多最優解
較多最優解若且唯若 並且
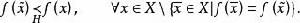 較多最優解
較多最優解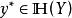 較多最優解
較多最優解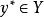 較多最優解
較多最優解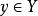 較多最優解
較多最優解(2) 若且唯若 並且不存在 使得
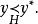 較多最優解
較多最優解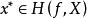 較多最優解
較多最優解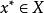 較多最優解
較多最優解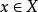 較多最優解
較多最優解若且唯若 並且不存在 使得
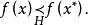 較多最優解
較多最優解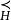 較多最優解
較多最優解從此定理可以知道,多目標規劃問題(VMP) 的較多有效解和較多最優解也即在嚴格偏愛“ ”意義下的最優解和非劣解。因此,它們也可分別叫做問題(VMP)的 強較多最優解和 弱較 多有效解。
定理4 任一較多有效點(解)必是較多最優點(解),並且它們都是Pareto有效點(解)。
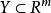 較多最優解
較多最優解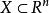 較多最優解
較多最優解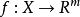 較多最優解
較多最優解定理5設 和 是非空集合, ,
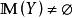 較多最優解
較多最優解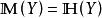 較多最優解
較多最優解(1) 若 ,則 。
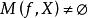 較多最優解
較多最優解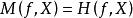 較多最優解
較多最優解(2) 若 ,則 。
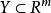 較多最優解
較多最優解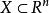 較多最優解
較多最優解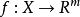 較多最優解
較多最優解定理6設 和 是非空集合, ,
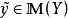 較多最優解
較多最優解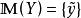 較多最優解
較多最優解(1) 若 ,則 。
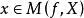 較多最優解
較多最優解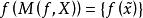 較多最優解
較多最優解(2) 若 ,則 。
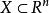 較多最優解
較多最優解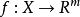 較多最優解
較多最優解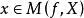 較多最優解
較多最優解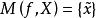 較多最優解
較多最優解定理7設 是非空凸集, 是嚴格凸向量函式,若 ,則 。

