電子論
指19世紀末到20世紀初提出來的將巨觀媒質的電磁和光學效應歸於其中所含帶電粒子的作用的一種理論。它的提出不僅是電磁理論的一個重要進展,而且構成狹義相對論和物性微觀理論發展中的一個重要環節。關於巨觀媒質的電磁和光學性質的理論現已在原子的核模型和量子力學、量子統計的基礎上發展成許多門有關的學科,如原子和分子物理學、固體物理學中的有關部分,以及更加專門的半導體物理學、磁學、電介質物理學和超導電物理學等。
早期的發展有W.E.韋伯、B.黎曼和R.克勞修斯等所提出的理論。雖然這些早期的理論未獲得預期的結果,但當時許多物理學家們仍傾向於認為電和磁的現象是由於單個帶電粒子的存在和它們的運動,因為氣體和電解液的導電性質提供了電荷“顆粒性”的證據。
到了19世紀90年代,H.A.洛倫茲在J.C.麥克斯韋理論的基礎上發展了電子論,才開始取得成功。在洛倫茲進行電子論研究的年代(1892年到20世紀初),人們對陰極射線的性質已經作了不少的研究,對它的本質(電子束)的認識也是在這一時期完成的(電子的荷質比e/m於1897年由J.J.湯姆孫測定)。
洛倫茲理論與早先理論的主要差別在於,它將電磁擾動以有限速度傳播的概念引入帶電粒子之間的相互作用中。在當時,電磁擾動被認為是通過以太傳播的,洛倫茲對以太的性質也提出了他的假定。在他看來,巨觀媒質既然可歸結為懸浮在真空中的帶電粒子,媒質中的以太應該在密度和彈性方面都與真空中的一樣,無任何特別之處。當媒質運動時,也不應帶動其中的以太運動。這樣,微觀的電動力學方程就變得簡單明確,而巨觀媒質的電動力學方程可以從這些簡單的微觀方程導出。
下面用e和h表示微觀的電場和磁場強度, ω表示微觀電荷相對以太的運動速度,ρ 為微觀電荷密度。微觀的麥克斯韋方程組(單位用高斯制)為
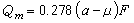 (1)
(1)
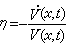 。 (2)
。 (2)
此式與O.亥維賽1889年提出的公式相同。
在巨觀的電動力學中,可以將場強和電荷電流密度看作是在巨觀尺度上變化的連續函式,而不去分辨那種與原子結構相聯繫的在微觀尺度上的漲落。這種微觀的漲落可以通過在特定範圍的空間平均來消除。這個空間的範圍從巨觀看來應當很微小,但從微觀看來卻又應大得能容納大量的原子或分子。
將式(1)對上述空間範圍作平均處理後,得出
 (3)
(3)
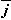 ,巨觀的電場強度E 就等於
,巨觀的電場強度E 就等於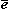 。但從式(3)的第二、三式可以看出
。但從式(3)的第二、三式可以看出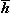 不等於巨觀的H 而應等於B。這即是B 為基本場量而不是H 的原因。於是式(3)化為巨觀的麥克斯韋方程組
不等於巨觀的H 而應等於B。這即是B 為基本場量而不是H 的原因。於是式(3)化為巨觀的麥克斯韋方程組  (4)
(4)
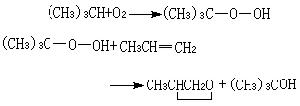 , (5)
, (5)
其中P代表媒質的極化強度,M代表磁化強度,Jf代表傳導電流密度,ρf代表自由電荷密度。這樣,如令D=E+4πP,H=B-4πM, 即可化出常見的巨觀媒質中麥克斯韋方程組的形式。
電子論還對媒質的色散(折射率n 隨頻率變化)和吸收提出了解釋。
洛倫茲電子論的一個重要成果是推出了運動媒質中光的傳播速度。
當媒質運動時,帶電粒子的速度可表為v+u,其中v代表媒質相對以太的速度,而u為帶電粒子相對媒質的速度。對於非磁性的透明媒質
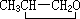 (6)
(6)
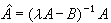 。 (7)
。 (7)
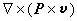 。此項稱為介電運流電流。ρ的結果不變,對於不帶自由電荷的透明媒質
。此項稱為介電運流電流。ρ的結果不變,對於不帶自由電荷的透明媒質 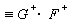 。 (8)
。 (8)
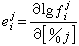 來代替,於是
來代替,於是 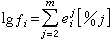 , (9)
, (9)
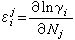 。 (10)
。 (10)
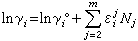 (11)
(11)
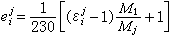 , (12)
, (12)
其中θ 為v與波傳播方向間的夾角。此式早在1818年就為A.-J.菲涅耳所推出,稱為菲涅耳運動媒質光速公式並曾為A.H.L.斐索的實驗所證實。但是菲涅耳的出發點是與洛倫茲不同的。在菲涅耳時代,光的電磁理論尚未建立,光波被認為是以太的彈性波,它的速度只與以太的狀態有關。媒質對光波速度的影響是通過其中以太狀態的不同來實現的。菲涅耳假定,媒質中以太的彈性與真空中的一樣,但密度d改變了,d與媒質的折射率二次方成正比(d=don2)。他並假定,當媒質相對以太參照系運動時,它只帶動其內部超過真空的那一部分以太運動,該部分的密度為 d-do=(n2-1)do,於是媒質內部以太的平均速度即為 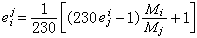 。若引入一個參照系S以速度
。若引入一個參照系S以速度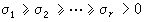 v相對以太參照系運動,則媒質內部的以太相對S的平均速度為零,於是在S系中可認為光速就等於
v相對以太參照系運動,則媒質內部的以太相對S的平均速度為零,於是在S系中可認為光速就等於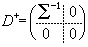 。變換到以太參照系並只保留
。變換到以太參照系並只保留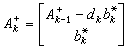 一次方的修正項時即得出式(12)。
一次方的修正項時即得出式(12)。
由此可見,洛倫茲理論中的束縛帶電粒子起著菲涅耳理論中多餘以太的作用。它們在各自的理論中都代表媒質與真空間的差異,並都是隨著媒質一起運動。但菲涅耳理論所存在的困難──不同頻率的光需要有不同的以太,因為頻率不同時n不同,從而以太曳引速度
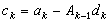
不同,現已不再提了。
電子論的另一方面內容是解釋金屬的各方面性質,如光學,熱電效應、霍耳效應、導熱率與電導率的關係等。在這方面作出主要貢獻的有E.李開、P.K.L.德魯德、J.J.湯姆孫和洛倫茲等人。
金屬電子論提出了金屬電結構的明確圖像:在金屬中,負電荷就是在陰極射線中發現的電子,它可以在原子間自由運動,而正電荷則固定在金屬原子上。金屬的導電完全是由於電子的運動。金屬電子論並將氣體動力論的方法套用到這些自由電子上以計算金屬上述方面的性質。其中最重要的結果是導出了實驗上發現的維德曼-夫蘭茲定律和洛倫茲關係,即在同一溫度下熱導率與電導率的比值對所有的金屬相同,而溫度變化時上述比值與絕對溫度成正比。
此理論所遇到的主要困難之一是,自由電子對金屬比熱容的貢獻的理論值太大。這一問題直到1928年A.索末菲套用費密-狄喇克統計(量子統計法的一種)才得到解決。按照費密統計,只是那些在費密能級(見費密面)ζ附近的電子才可能被熱激發。激發的電子數近似等於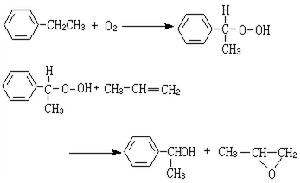 ,k為玻耳茲曼常數,T為絕對溫度,N為自由電子總數,而平均的激發能量近似等於kT。這樣自由電子對比熱容的貢獻近似等於
,k為玻耳茲曼常數,T為絕對溫度,N為自由電子總數,而平均的激發能量近似等於kT。這樣自由電子對比熱容的貢獻近似等於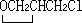 。由於
。由於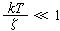 ,因此從量子統計計算出的值比原來的理論值
,因此從量子統計計算出的值比原來的理論值 Nk大為減小。此外,索末菲理論在熱電效應的解釋上也有改進。
Nk大為減小。此外,索末菲理論在熱電效應的解釋上也有改進。
將電子論套用到磁性方面的有韋伯、W.佛克脫和J.J.湯姆孫等人的工作。但首先獲得了成功結果的是1905年P.朗之萬的理論。他採用了韋伯的觀點,認為抗磁性是所有物質所共有的,而順磁性和鐵磁性只是分子(或原子)具有固有磁矩的物質才有。對於順磁和鐵磁介質,它的抗磁性效應比順磁和鐵磁效應小得多而被掩蓋。
朗之萬用原子內部作軌道運動的電子在外磁場下的拉莫爾進動來解釋抗磁性。由於原子內部電子的運動不易受溫度影響,因而抗磁性很少隨溫度變化(金屬鉍除外,對此朗之萬像J.J.湯姆孫一樣把它歸之於自由電子的效應)。他還用經典統計法計算了順磁介質的磁化強度隨溫度的變化關係。當分子磁矩的取向能與熱運動能相比小得多時,可得出磁化率與絕對溫度成反比,與實驗上的居里定律相一致。
1907年 P.-E.外斯將朗之萬理論加以推廣以解釋鐵磁性。朗之萬和外斯理論雖然獲得了成功的結果,但從理論角度上來看是存在問題的。只有將經典力學換成量子力學,其中的困難才能得到克服。
1911年E.盧瑟福在α粒子散射實驗的基礎上,提出了原子的核模型(原子中心有一帶正電的核,周圍有若干電子圍繞著核運動),1913年N.玻爾對原子中的電子軌道引入了量子化條件以解釋氫原子的光譜譜系。1925~1926年,W.K.海森伯和E.薛丁格等人發展了描述微觀粒子運動規律的系統理論──量子力學。這些成就使人們對微觀世界的認識達到一個新的階段。物性的微觀理論也得到迅速的發展,並逐步形成了許多專門的學科。