雷其極點

散射振幅在角動量複平面上的極點。這種極點的位置隨能量的改變而變動。散射振幅幾乎包含了散射問題的全部信息。二體彈性散射的散射振幅是體系的能量 E和角動量 l的函式。

正文

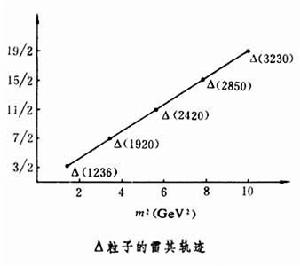
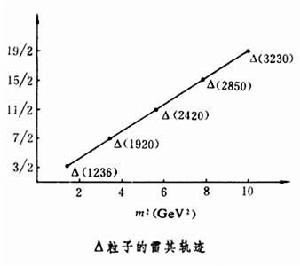
在20世紀50年代末期, 義大利的T.雷其深入細緻地研究了散射振幅的性質，發現對於通常所涉及的、具有良好行為的作用勢，其散射振幅均可延拓到 l的複平面上去(Rel≥-n)，並且在l複平面上可能具有極點。這種極點稱為雷其極點。位於 l等於正整數附近的雷其極點就對應體系的束縛態（或共振態）,其極點位置在l複平面上的虛部（大於零）與該束縛態的寬度有關。
體系能量E 變更時,雷其極點的位置也隨之移動,由此在 l複平面上所畫出的軌跡稱為雷其軌跡。這種軌跡反映出體系的共振態的能量與角動量的關係。後來雷其極點和雷其軌跡的概念被推廣到量子場論的 S 矩陣中去，並在粒子物理學中得到廣泛套用，實驗發現：具有相同內部量子數（如同位旋、奇異數）的低質量強子的能量和自旋J的關係,都在一條直線的雷其軌跡上。而所有低質量強子的雷其軌跡是一組幾乎平行的直線，Δ 粒子的雷其軌跡(m為質量)如圖所示。這一現象含有關於強子結構的深刻意義，受到人們的普遍重視。

雷其極點

通常用分波相移法來分析低能散射實驗，但對高能散射，此法實際上失效。雷其極點理論提供了一種分析高能散射實驗的方法，對散射過程a+b→c+d存在交叉過程a+廀→c+姼、其中姼、廀分別為b和d的反粒子,後一過程稱前一過程的交叉道。雷其極點理論認為高能散射實驗可用交叉道的主導的雷其極點的位置及在此極點處散射振幅的留數來分析。這些也是近來分析高能散射實驗時常用的物理參量。為了解釋很高能量的實驗，除了引進雷其極點項外，人們還建議引進散射振幅在復角動量平面上的割線項，這種割線稱為雷其割線。在雷其極點理論基礎上發展起來的對偶共振理論，也是分析高能散射的理論工具之一。