基本介紹
垂極點曾被紐堡(Neuberg),松恩(Soons),蓋拉特雷(Gallatly)等人廣泛研究,最後由蓋拉特雷集其大成。
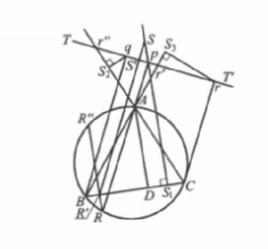
定理 設由一個三角形的各個頂點向任一條直線作垂線,則由其垂足向對邊所作垂線必交於一點,稱為這條直線的 垂極點。當直線平行移動時,垂極點的軌跡是與它垂直的直線。與外接圓相交的直線,垂極點是交點的西摩松線的交點。換句話說。一點的西摩松線是過這點的各條直線的垂極點的軌跡。如果一條直線通過外心,那么它的垂極點在九點圓上。
設一條直線交外接圓於P,Q,由三角形的頂點作這條線的垂線,每條垂線與外接圓還有一個交點,從這些交點向對邊作垂線,則這些垂線相交於外接圓上一點R。由PQ上的三個垂足向對邊作垂線,這些垂線相交於垂極點S。而P,Q,R的西摩松線也都通過S,S是直線PQ,PR,QR中任一個的垂極點。
一條直線的垂極點,關於這條線上所有點的垂足圓,有相同的冪 。
相關研究及結論
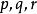 垂極點
垂極點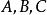 垂極點
垂極點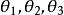 垂極點
垂極點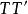 垂極點
垂極點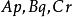 垂極點
垂極點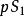 垂極點
垂極點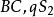 垂極點
垂極點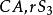 垂極點
垂極點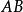 垂極點
垂極點❶設 為 到一條方向角為 的直線 的垂線 的長。作 垂直於 垂直於 垂直於 。這三條直線必定共點。
因為
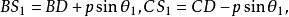 垂極點
垂極點且
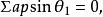 垂極點
垂極點所以
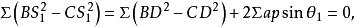 垂極點
垂極點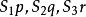 垂極點
垂極點因此 共點。
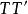 垂極點
垂極點這公共點記為S,紐堡(J.Neuberg)教授將它稱為 的 垂極點 。
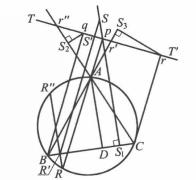 圖1
圖1原註:垂極點的定理幾乎全屬於J.Neuberg教授。
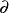 垂極點
垂極點 垂極點
垂極點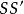 垂極點
垂極點設 為 到TT' 的垂線 的長。
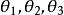 垂極點
垂極點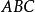 垂極點
垂極點取一特殊情況,以 表示TT' 與 的邊所成的銳角。我們有
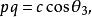 垂極點
垂極點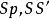 垂極點
垂極點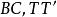 垂極點
垂極點又因為 垂直於
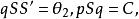 垂極點
垂極點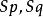 垂極點
垂極點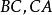 垂極點
垂極點同樣因為 垂直於
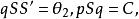 垂極點
垂極點所以
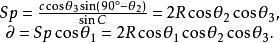 垂極點
垂極點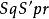 垂極點
垂極點當TT' 平行移動時,圖形 的形狀與大小均保持不變。
❷ 用幾何方法確定垂極點。
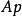 垂極點
垂極點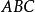 垂極點
垂極點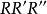 垂極點
垂極點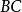 垂極點
垂極點設 再交圓 於R,作弦 垂直於 。
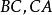 垂極點
垂極點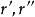 垂極點
垂極點設 交TT' 於 ,則
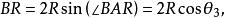 垂極點
垂極點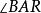 垂極點
垂極點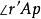 垂極點
垂極點( 即 )
同樣
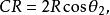 垂極點
垂極點所以
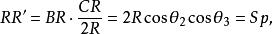 垂極點
垂極點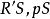 垂極點
垂極點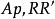 垂極點
垂極點因此作 平行於 ,便得到S。
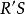 垂極點
垂極點當TT' 平行移動時,S沿TT' 的垂線 移動。
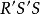 垂極點
垂極點平行於AR,是R''的西摩松線。
❸確定S對於ABC的n.c.。
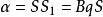 垂極點
垂極點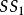 垂極點
垂極點因為 在 上的射影=
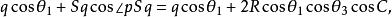 垂極點
垂極點所以
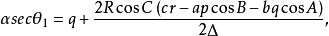 垂極點
垂極點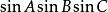 垂極點
垂極點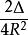 垂極點
垂極點將上式右邊第一項乘以 ,其他項乘以 ,得
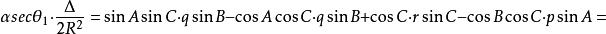 垂極點
垂極點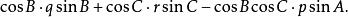 垂極點
垂極點又
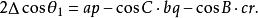 垂極點
垂極點所以
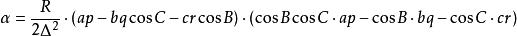 垂極點
垂極點將上式右邊的兩個因式相乘,並利用
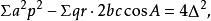 垂極點
垂極點得
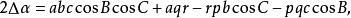 垂極點
垂極點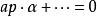 垂極點
垂極點 垂極點
垂極點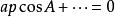 垂極點
垂極點TT' 的方程為 ,在它通過圓心 時,有 ,此時
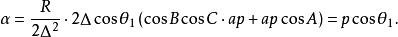 垂極點
垂極點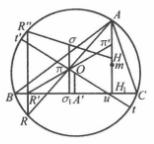 圖2
圖2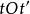 垂極點
垂極點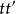 垂極點
垂極點 垂極點
垂極點❹設 為與TT' 平行的直徑,則 的垂極點 在九點圓上。
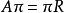 垂極點
垂極點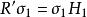 垂極點
垂極點證明:令H為ABC的垂心,因為 ,所以 。
又
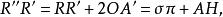 垂極點
垂極點所以
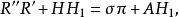 垂極點
垂極點但
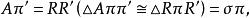 垂極點
垂極點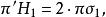 垂極點
垂極點所以
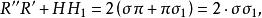 垂極點
垂極點 垂極點
垂極點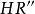 垂極點
垂極點因此是的中點,從而在九點圓上。
 垂極點
垂極點❺圓ABC的任一弦TT'的端點的西摩松線,過TT'的垂極點。
❻ 萊莫恩定理:
 垂極點
垂極點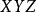 垂極點
垂極點若是直線TT'上一點,TT'的垂極點為S,則S關於P的垂足圓的冪為常數。
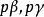 垂極點
垂極點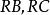 垂極點
垂極點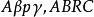 垂極點
垂極點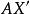 垂極點
垂極點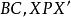 垂極點
垂極點 垂極點
垂極點作平行於,圓位似,作平行於垂直於。
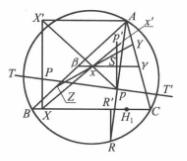 圖3
圖3 垂極點
垂極點 垂極點
垂極點 垂極點
垂極點❼在TT'為外接圓直徑時,d為0,這時垂足三角形都過的垂極點。
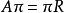 垂極點
垂極點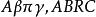 垂極點
垂極點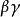 垂極點
垂極點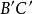 垂極點
垂極點因為在這時,。位似圖形的比是1:2,所以變為。
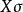 垂極點
垂極點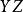 垂極點
垂極點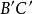 垂極點
垂極點因此與在上相交 。