簡介
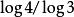 科赫曲線
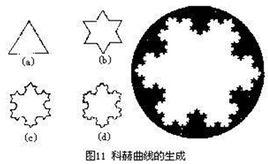
科赫曲線 科赫曲線是一種分形。其形態似雪花,又稱 科赫雪花、雪花曲線。其豪斯多夫維是。它最早《關於一條連續而無切線,可由初等幾何構作的曲線》(1904年,法語原題: Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire)。
科赫曲線是de Rham曲線的特例。
1.給定線段AB,科赫曲線可以由以下步驟生成:
2.將線段分成三等份(AC,CD,DB)
3.以CD為底,向外(內外隨意)畫一個等邊三角形DMC
4.將線段CD移去
分別對AC,CM,MD,DB重複1~3。
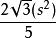 科赫曲線
科赫曲線 科赫雪花是以等邊三角形三邊生成的科赫曲線組成的。科赫雪花的面積是,其中S是原來三角形的邊長。每條科赫曲線的長度是無限大,它是連續而無處可微的曲線。
記錄
以L系統:
字元 : F
常數 : +, −
公理 : F++F++F
規則: F → F−F++F−F
F :向前
- :左轉60°
+ :右轉60°
畫法
1、任意畫一個正三角形,並把每一邊三等分;
2、取三等分後的一邊中間一段為邊向外作正三角形,並把這“中間一段”擦掉;
3、重複上述兩步,畫出更小的三角形。
4、一直重複,直到無窮,所畫出的曲線叫做科赫曲線。
和皮亞諾類似:
1、曲線任何處不可導,即任何地點都是不平滑的
2、總長度趨向無窮大
3、曲線上任意兩點沿邊界路程無窮大
4、面積是有限的
5、產生一個匪夷所思的悖論:"無窮大"的邊界,包圍著有限的面積。(保守派數學大師們暈倒撞牆去吧)
Kohn曲線是比較典型的分形圖形,它具有嚴格的自相似特性。