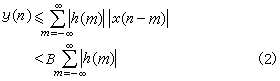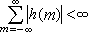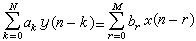離散時間系統的時域分析

)是系統的輸入序列；y(n )產生的回響等於系統的單位衝激回響h(n 離散時間系統的穩定性

離散時間系統的時域分析

正文

在時域中研究輸入作用於系統而產生輸出的問題。例如給定系統的數學模型、起始狀態及輸入序列，在時域中直接求出系統的輸出。時域分析不藉助任何變換而直接求解，它概念清晰，但在分析複雜系統時，計算工作量較大。
零狀態回響和零輸入回響　線性時不變離散時間系統是用常係數線性差分方程來描述的。對單輸入單輸出的系統，方程的一般形式是

　 (1)

　式中χ(n)是系統的輸入序列；y(n)是系統的輸出序列；N為系統的階次;ak、br都是常數,k=0,1,2,…,N、a0≠0,r=0,1,2,…,M。給定系統的方程(1)以及系統的初始條件y(0),y(1),…,y(N-1),便可以用求解常係數線性差分方程的方法求式 (1)的解。最簡單的解法是疊代法。這種算法尤其適用於用計算機去執行。用經典的求常係數線性差分方程解的方法與求相對應的微分方程解方法相似。它包括求齊次方程的通解和求非齊次方程的特解。這兩部分解之和就是其通解。用初始條件決定其中的積分常數,就得到滿足方程(1)及滿足給定初始條件的特解。
可以將給定初始條件描述的方程 (1)的解分成零狀態回響和零輸入回響兩部分來求。前者是方程 (1)滿足初始條件為零的特解;後者是方程(1)的齊次方程滿足給定初始條件的特解。兩者之和即為所求的全回響。
衝激回響　線性時不變系統對單位衝激δ(n)作用在零狀態條件下的回響稱為衝激回響h(n)。單位衝激函式的定義是

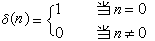
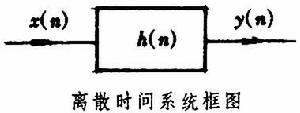離散時間系統常以框圖表示(見圖)。圖中χ(n)、y(n)分別為系統的輸入和輸出。系統的衝激回響可以通過令式(1)中右端的激勵為δ(n)求得。
線性時不變離散時間系統有時不變和線性性質，只要知道系統在任一激勵下的回響，就可以決定它在任何激勵下的回響。對於線性時不變離散時間系統，在零狀態下，任意一激勵χ(n)產生的回響等於系統的單位衝激回響h(n)與激勵的卷積，即

當χ(n)和h(n)是長序列時,用上式計算輸出y(n)，計算工作量是很大的。因此，常使用DFT的快速算法(FFT)計算卷積。
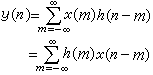
離散時間系統的穩定性　任意有界輸入產生有界輸出的系統稱為穩定系統。要使系統具有穩定性質，則要對系統提出一些約束條件。
對於有限衝激回響系統，因為當m＞N（N為有限值）時, h(m)呏0，只要每個h(m)都是有界的,則有界輸入必產生有界輸出，系統必然是穩定的。
對有無限衝激回響系統，情況與上述有所不同。由於輸入是有界的，可設|χ(n)|＜B,B為大於最大輸入幅值的某個固定值，於是有

　y(n)有界要求式(2)右側有界，所以要求

換句話說，無限衝激回響系統必須在其單位衝激回響絕對可和的條件下才是穩定的。

配圖

相關連線